
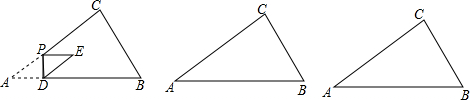
分析 (1)由勾股定理和平行线的判定与性质解答;
(2)需要分类讨论:DE=EB、BD=DE和BE=BD三种情况.
解答 解:(1)由题意,∠C=90°,AC=8,BC=6,
∴AB=10
∵AP=DE=x,
∴AD=PE=$\frac{4}{5}$x,PD=$\frac{3}{5}$x,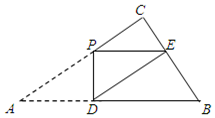
点E落在边BC上,PE∥AB,
∴$\frac{CP}{AC}$=$\frac{PE}{AB}$,
∴$\frac{8-x}{8}$=$\frac{4x}{50}$,
∴x=$\frac{200}{41}$;
(2)∵△EDB为等腰三角形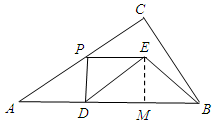
①若DE=EB(如图)作EM⊥AB于M,则DM=$\frac{1}{2}$DB=PE=AD=$\frac{10}{3}$,
∴$\frac{4}{5}$x=$\frac{10}{3}$,
∴x=$\frac{25}{6}$,
∴AP=$\frac{25}{6}$.
②若BD=DE(如图)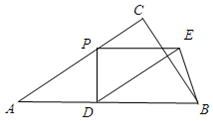
x=10-$\frac{4}{5}$x,解之x=$\frac{50}{9}$,
∴AP=$\frac{50}{9}$.
③若BE=BD(如图)
∵DE∥AC,
∴DE⊥BC,
又∵BE=BD,
∴DN=$\frac{1}{2}$DE=$\frac{1}{2}$AP=$\frac{1}{2}$x
∵Rt△ADP∽Rt△DNB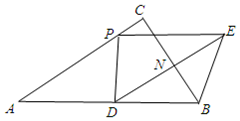
∴$\frac{AP}{BD}$=$\frac{AD}{DN}$,即$\frac{x}{10-\frac{4}{5}x}$=$\frac{\frac{4}{5}x}{\frac{1}{2}x}$,
∴x=$\frac{400}{57}$,
∴AP=$\frac{400}{57}$,
综上,当AP=$\frac{25}{6}$、$\frac{50}{9}$、$\frac{400}{57}$时,△EDB为等腰三角形.
点评 本题考查了旋转的性质,勾股定理以及等腰三角形的判定.解题时,注意“分类讨论”数学思想的应用.


科目:初中数学 来源: 题型:解答题
| 数量范围(千克) | 0~50 部分(包括50) | 50以上~150 部分(包括150) | 150以上~250 部分(包括250) | 250以上 部分 |
| 价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
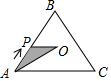 如图,在等边△ABC中,点O是中心,点P从点A出发,沿着等边三角形的边顺时针方向运动一周,则△APO的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )
如图,在等边△ABC中,点O是中心,点P从点A出发,沿着等边三角形的边顺时针方向运动一周,则△APO的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )| A. | 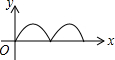 | B. | 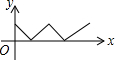 | C. | 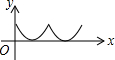 | D. | 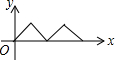 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
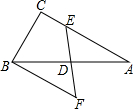 如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )
如图,Rt△ABC中,∠C=90°,∠A=30°,BC=1,D为AB中点,E为AC上一动点,BF∥C交ED延长线于点F,则四边形BCEF周长的最小值为( )| A. | 1+$\sqrt{3}$ | B. | 4 | C. | 2+$\sqrt{3}$ | D. | 2+$\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
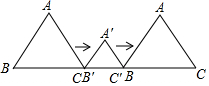 如图,边长为4的等边△ABC和边长为2的等边△A′B′C′的位置如图所示,它们的边BC、B′C′位于同一条直线l上,点C与B′重合,△A′B′C′固定不动,然后把△ABC自左向右沿直线l平移,移出△A′B′C′外(点B与C′重合)停止,设△ABC平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )
如图,边长为4的等边△ABC和边长为2的等边△A′B′C′的位置如图所示,它们的边BC、B′C′位于同一条直线l上,点C与B′重合,△A′B′C′固定不动,然后把△ABC自左向右沿直线l平移,移出△A′B′C′外(点B与C′重合)停止,设△ABC平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )| A. | 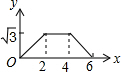 | B. | 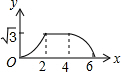 | C. | 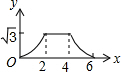 | D. | 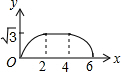 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
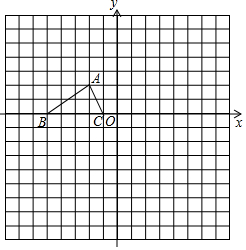 如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0),P(a,b)是△ABC的边AC上一点:
如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0),P(a,b)是△ABC的边AC上一点:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
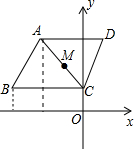 如图,平行四边形ABCD的顶点A(-2,3),B(-3,1),C(0,1),规定“平行四边形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,则连续经过2017次变换后,平行四边形ABCD的对角线的交点M的坐标为( )
如图,平行四边形ABCD的顶点A(-2,3),B(-3,1),C(0,1),规定“平行四边形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,则连续经过2017次变换后,平行四边形ABCD的对角线的交点M的坐标为( )| A. | (-2017,2) | B. | (-2017,-2) | C. | (-2018,-2) | D. | (-2018,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com