
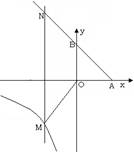
��ͼ����֪����������y�� ����P�� P�������Ϊ��3��m��2m����m�Ƿ�ʽ����
����P�� P�������Ϊ��3��m��2m����m�Ƿ�ʽ���� �Ľ⣬PA��x���ڵ�A��PB��y���ڵ�B.
�Ľ⣬PA��x���ڵ�A��PB��y���ڵ�B.
��1�����ж��ı���PAOB����״����˵�����ɣ�

��2������AB��EΪAB�ϵ�һ�㣬EF��BP�ڵ�F��GΪAE���е㣬����OG��FG������FG��OG�к�������ϵ����д����Ľ��۲�֤��.

��3����MΪ����������y�� �ڵ��������ڵ�һ���㣬��M��MN��x���ڽ�AB���ӳ����ڵ�N���Ƿ����һ��Mʹ���ı���OMNBΪ�������Σ������ڣ������M������ꣻ�������ڣ���˵������.
�ڵ��������ڵ�һ���㣬��M��MN��x���ڽ�AB���ӳ����ڵ�N���Ƿ����һ��Mʹ���ı���OMNBΪ�������Σ������ڣ������M������ꣻ�������ڣ���˵������.

�⣺��1���ı���PAOB��������.��������
�ߡ�AOB=��OBP=��OAP=90��
���ı���PAOB�Ǿ���
m��3��m��2=��3
��ã�m=1
������֪m=1��ԭ��ʽ���̵Ľ�
��P��2��2��
��PB=PA=2
���ı���PAOB��������.
��2��OG=FG.֤�����£�
�ӳ�FE��OA�ڵ�H������GH

�ߡ�HFB =��FBO=��BOH=90��
��BOHF�Ǿ���
��BF=OH
�ߡ�FBE=��FEB=45��
��EF= BF=OH
�ߡ�EHA=90�㣬GΪAE���е�
��GH=GE=GA
���GEH=��GAH=45��
���GEF=��GHO
���GEF�ա�GHO
��OG=FG
��3��������֪����BNM=45��
��Ҫ���ı���OBNMΪ��������
���BNM=��NMO=45��
����M���������x,x��������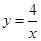
��x=��2
��M��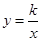 ����������һ����
����������һ����
��x=-2
��M���������-2,-2��
����������1�������ʽ���̵õ�m��ֵ���������жϳ��ı���PAOB����״��
��2��Ӧ������ȣ����������߶�����������ȫ�ȵ�������
��3����֪��BNM=45�㣬Ҫ��Ϊ�������Σ���OMN=45�㣬��ô��M�ĺ���������ȣ����뷴�����������ɣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪����������y=
��ͼ����֪����������y=| m |
| x |
| 4 |
| 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪����������y=
��ͼ����֪����������y=| k | x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪����������y=
��ͼ����֪����������y=| k | x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪����������y1=
��ͼ����֪����������y1=| k | x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪����������y=
��ͼ����֪����������y=| k |
| x |
| k |
| x |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com