
【题目】老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:![]() +(﹣3x2+5x﹣7)=﹣2x2+3x﹣6
+(﹣3x2+5x﹣7)=﹣2x2+3x﹣6
(1)求所捂的多项式;
(2)若x是![]() x=﹣
x=﹣![]() x+3的解,求所捂多项式的值;
x+3的解,求所捂多项式的值;
(3)若x为正整数,x每取一个值,都可以求出所捂多项式的值,请你任取x的几个值(不要写在答题纸上),发现它们之间有一定的规律,请用含x的式子表示这一结论:____________=_____________;
(4)若所捂多项式的值为729,请直接写出x的取值.
【答案】(1)![]() ;(2)x=4, 9;(3)
;(2)x=4, 9;(3)![]() .(4)28或-26
.(4)28或-26
【解析】
(1)根据题意列出整式相减的式子,再去括号,合并同类项即可;
(2)先求出方程的解,然后代入(1)中求得的所捂的多项式即可;
(3)令x=1,2,3,4求出所捂多项式的值,找出规律即可;
(4)根据第(3)问发现的规律进行计算即可.
解:(1)﹣2x2+3x﹣6﹣(﹣3x2+5x﹣7)=﹣2x2+3x﹣6+3x2-5x+7=x2-2x+1,
即所捂的多项式是:x22x+1;
(2)解方程![]() x=﹣
x=﹣![]() x+3,得x=4,
x+3,得x=4,
∴x22x+1=422×4+1=9,
即若x是![]() x=﹣
x=﹣![]() x+3的解,所捂多项式的值是9;
x+3的解,所捂多项式的值是9;
(3)当x=1时,x22x+1=12+1=0;
当x=2时,x22x+1=44+1=1;
当x=3时,x22x+1=96+1=4;
当x=4时,x22x+1=168+1=9,…,
由上可以发现规律是所捂多项式的值是代入的正整数x减去1所得结果的平方,
即x22x+1 =(x-1)2;
(4)若所捂多项式的值为729,则(x-1)2=729,
∴x-1=±27,
∴x的值是28或-26.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】某商场欲购进果汁饮料和碳酸饮料共60箱,两种饮料每箱的进价和售价如下表所示。设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为W元(注:总利润=总售价-总进价)。
(1)设商场购进碳酸饮料y箱,直接写出y与x的函数解析式;
(2)求总利润w关于x的函数解析式;
(3)如果购进两种饮料的总费用不超过2100元,那么该商场如何进货才能获利最多?并求出最大利润。
饮料 | 果汁饮料 | 碳酸饮料 |
进价(元/箱) | 40 | 25 |
售价(元/箱) | 52 | 32 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件个数定为260,你认为这个定额是否合理?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强打算找印刷公司设计一款新年贺卡并印刷.如图1是甲印刷公司设计与印刷卡片计价方式的说明(包含设计费与印刷费),乙公司的收费与印刷卡片数量的关系如图2所示.
(1)分别写出甲乙两公司的收费y(元)与印刷数量x之间的关系式.
(2)如果你是小强,你会选择哪家公司?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正方形ABCD中,点E、F、G分别是边AD、AB、BC的中点,连接EP、FG.
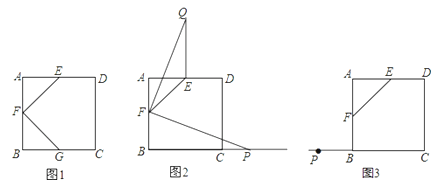
(1)如图1,直接写出EF与FG的关系____________;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转90°,得到线段FH,连接EH.
①求证:△FFE≌△PFG;②直接写出EF、EH、BP三者之间的关系;
(3)如图3,若点P为CB延长线上的一动点,连接FP,按照(2)中的做法,在图(3)中补全图形,并直接写出EF、EH、BP三者之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角尺按如图所示的方式拼在一起,已知∠BCE=25°.
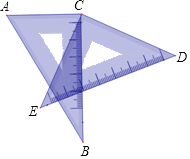
(1)图中∠ACE= 度,∠DCB= 度;
(2)求∠ACD+∠BCE的度数;
(3)如果去掉条件“∠BCE=25°”.那么(2)中的结论还成立吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点![]() 出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到
出发,按向上.向右.向下.向右的方向依次平移,每次移动一个单位,得到![]() (0,1),
(0,1),![]() (1,1),
(1,1),![]() (1,0),
(1,0),![]() (2,0),…那么点
(2,0),…那么点![]() 的坐标为__________.
的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】织金县某中学300名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
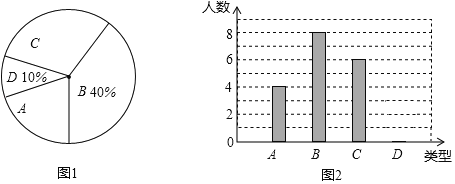
(1)在这次调查中D类型有多少名学生?
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这300名学生共植树多少棵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com