
分析 ①设该同学看中的随身听的单价为x元/台,书包单价为y元/个,根据“随身听与书包的单价和是452元,且随身听的单价是书包的单价的4倍少8元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
②根据A、B超市促销方式,分别求出购买两样物品的总钱数,比较后即可得出结论.
解答 解:①设该同学看中的随身听的单价为x元/台,书包单价为y元/个,
根据题意得:$\left\{\begin{array}{l}{x+y=452}\\{x=4y-8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=360}\\{y=92}\end{array}\right.$.
答:该同学看中的随身听的单价为360元/台,书包单价为92元/个.
②在A超市购物的总费用为452×0.8=361.6(元),
在B超市购物,先花360元购买随身听,将得到90元的购物卷,再拿购物券和2元钱购买书包,花费的总钱数为:360+(92-90)=362(元),
∵361.6<362,
∴在A超市购物总花费少些.
答:他在A超市买更省钱.
点评 本题考查了二元一次方程组的应用,解题的关键是:①找准等量关系,列出二元一次方程组;②根据促销方式,分别求出在两超市购物需花总钱数.


科目:初中数学 来源: 题型:填空题
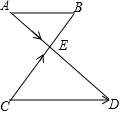 如图,已知AB∥CD,CD=2AB,AD、BC相交于点E,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{CE}$=$\overrightarrow{b}$,那么向量$\overrightarrow{CD}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为$\overrightarrow{b}$+2$\overrightarrow{a}$.
如图,已知AB∥CD,CD=2AB,AD、BC相交于点E,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{CE}$=$\overrightarrow{b}$,那么向量$\overrightarrow{CD}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为$\overrightarrow{b}$+2$\overrightarrow{a}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y3<y2,y1<y2 | B. | y1<y2<y3 | C. | y1>y2>y3 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
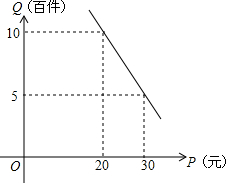 在精准对口扶贫活动中,甲单位将经营状况良好的某种专卖店以5.8万元的优惠价转让给了尚有5万元无息贷款还没有偿还的乙户,并约定从该店经营的利润中,首先保证乙户的一家人每月最低生活费的开支3600元后,逐步偿还转让费(不计利息).从甲单位提供的相关资料中可知这种消费品的进价是每件14元;月销售量Q(百件)与销售单价P(元)的关系如图所示;维持的正常运转每月需工资外的各种开支2000元.
在精准对口扶贫活动中,甲单位将经营状况良好的某种专卖店以5.8万元的优惠价转让给了尚有5万元无息贷款还没有偿还的乙户,并约定从该店经营的利润中,首先保证乙户的一家人每月最低生活费的开支3600元后,逐步偿还转让费(不计利息).从甲单位提供的相关资料中可知这种消费品的进价是每件14元;月销售量Q(百件)与销售单价P(元)的关系如图所示;维持的正常运转每月需工资外的各种开支2000元.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com