
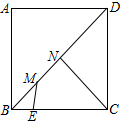
 在边长为5正方形ABCD中,点E是BC上,且BE=2,点M、N是对角线BD上两点,且MN=$\sqrt{2}$.当四边形CEMN周长最小时,则cos∠BCN的值$\frac{4}{5}$.
在边长为5正方形ABCD中,点E是BC上,且BE=2,点M、N是对角线BD上两点,且MN=$\sqrt{2}$.当四边形CEMN周长最小时,则cos∠BCN的值$\frac{4}{5}$. 分析 根据题意得出作EF∥BD且EF=$\sqrt{2}$,连结AF交BD于N,在BD上截取MN=$\sqrt{2}$,此时四边形CEMN的周长最小,进而利用相似三角形的判定与性质得出答案.
解答 解:作EF∥BD且EF=$\sqrt{2}$,连结AF交BD于N,在BD上截取MN=$\sqrt{2}$,延长AF交BC于P,作FQ⊥BC于Q,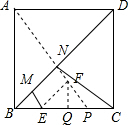 则四边形BMNE的周长最小,
则四边形BMNE的周长最小,
由∠FEQ=∠DBC=45°,可求得FQ=EQ=1,
∵∠APB=∠FPQ,∠ABP=∠FQP,
∴△PFQ∽△PAB,
∴$\frac{PQ}{PQ+EQ+BE}$=$\frac{FQ}{AB}$,
∴$\frac{PQ}{PQ+3}$=$\frac{1}{5}$,
解得:PQ=$\frac{3}{4}$,
∴PB=3+$\frac{3}{4}$=$\frac{15}{4}$,
由对称性可求得tan∠BCN=tan∠PAB=$\frac{\frac{15}{4}}{5}$=$\frac{3}{4}$.
∴cos∠BCN=$\frac{4}{5}$
故答案为$\frac{4}{5}$.
点评 此题主要考查了正方形的性质以及相似三角形的判定与性质,得出M,N的位置是解题关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
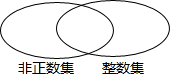 如图的两个圈分别表示非正数集和整数集,请在每个圈内填入六个数,其中三个数既在非正数集又在整数集内,你能用一个合适的语句来表示两个圈重叠部分的意义吗?
如图的两个圈分别表示非正数集和整数集,请在每个圈内填入六个数,其中三个数既在非正数集又在整数集内,你能用一个合适的语句来表示两个圈重叠部分的意义吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com