
【题目】已知点A(t,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)与y=x图象的交点.
(1)求t;
(2)若函数y=ax2+bx+4的图象与x轴只有一个交点,求a,b;
(3)若1≤a≤2,设当![]() ≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
【答案】(1)t=1;(2)![]() 或
或![]() ;(3)m﹣n的最小值
;(3)m﹣n的最小值![]()
【解析】
(1)把A(t,1)代入y=x即可得到结论;
(2)根据题意得方程组,解方程组即可得到结论;
(3)把A(1,1)代入y=ax2+bx+4得,b=3a,得到y=ax2(a+3)x+4的对称轴为直线x=![]() ,根据1≤a≤2,得到对称轴的取值范围
,根据1≤a≤2,得到对称轴的取值范围![]() ≤x≤2,当x=
≤x≤2,当x=![]() 时,得到m=
时,得到m=![]() ,当x=2时,得到n=
,当x=2时,得到n=![]() ,即可得到结论.
,即可得到结论.
解:(1)把A(t,1)代入y=x得t=1;
(2)∵y=ax2+bx+4的图象与x轴只有一个交点,
∴![]() ,
,
∴![]() 或
或![]() ;
;
(3)把A(1,1)代入y=ax2+bx+4得,b=﹣3﹣a,
∴y=ax2﹣(a+3)x+4=a(x﹣![]() )2﹣
)2﹣![]() ,
,
∴对称轴为直线x=![]() ,
,
∵1≤a≤2,
∴![]() ≤x=
≤x=![]() ≤2,
≤2,
∵![]() ≤x≤2,
≤x≤2,
∴当x= 当x=2时,n=﹣ ∴m﹣n= ∵1≤a≤2, ∴当a=2时,m﹣n的值最小, 即m﹣n的最小值![]() 时,y=ax2+bx+4的最大值为m=﹣
时,y=ax2+bx+4的最大值为m=﹣![]() ,
,![]() ,
,![]() ,
,![]() .
.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】某企业车间有技术工人20人,车间为了合理制定产品的每月生产定额,作了这20人某月加工零件个数的条形统计图.
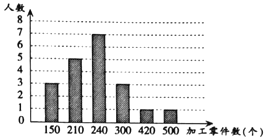
(1)写出这20人该月加工零件数的众数和中位数;
(2)计算这20人该月加工零件数的平均数;
(3)假如车间负责人把每位工人的月加工零件数定为260件,请你说明这个定额是否合理,如果不合理,请你确定一个比较合理的加工定额,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市民广场有一个直径16米的圆形喷水池,喷水池的周边有一圈喷水头(喷水头高度忽略不计),各方向喷出的水柱恰好在喷水池中心的装饰物OA的顶端A处汇合,水柱离中心3米处达最高5米,如图所示建立直角坐标系.王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的他站立时必须在离水池中心O________米以内.
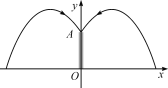
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)经过点(1,1)和(﹣1,0).下列结论:①a+c=1;②b2﹣4ac≥0;③当a<0时,抛物线与x轴必有一个交点在点(1,0)的右侧;④抛物线的对称轴为x=﹣![]() .其中结论正确的个数有( )
.其中结论正确的个数有( )
A.4 个B.3 个C.2 个D.1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
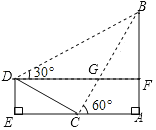
【题目】如图,小明想测量斜坡![]() 旁一棵垂直于地面
旁一棵垂直于地面![]() 的树
的树![]() 的高度,他们先在点
的高度,他们先在点![]() 处测得树顶
处测得树顶![]() 的仰角为
的仰角为![]() ,然后在坡顶
,然后在坡顶![]() 测得树顶
测得树顶![]() 的仰角为
的仰角为![]() ,已知斜坡
,已知斜坡![]() 的长度为
的长度为![]() ,斜坡顶点
,斜坡顶点![]() 到地面的垂直高度
到地面的垂直高度![]() ,则树
,则树![]() 的高度是( )
的高度是( )![]()
A. 20![]() B. 30
B. 30![]() C. 30D. 40
C. 30D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数![]() 都可以进行这样的分解,
都可以进行这样的分解,![]() (
(![]() ,
,![]() 是正整数且
是正整数且![]() ),在
),在![]() 的所有这种分解中,如果
的所有这种分解中,如果![]() ,
,![]() 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称![]() 是
是![]() 的最佳分解,并规定:
的最佳分解,并规定:![]() ,例如
,例如![]() 可以分解成
可以分解成![]() 、
、![]() 或
或![]() .因为
.因为![]() ,所有
,所有![]() 是最佳分解,所以
是最佳分解,所以![]() .
.
(1)求![]() .
.
(2)如果一个两位正整数![]() ,
,![]() (
(![]() ,
,![]() 、
、![]() 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为
为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为![]() ,那么我们称这个数
,那么我们称这个数![]() 为 “吉祥数”,求所有“吉祥数”中
为 “吉祥数”,求所有“吉祥数”中![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
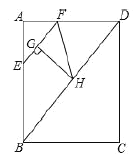
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,以每秒4个单位长度的速度沿边
出发,以每秒4个单位长度的速度沿边![]() 运动,到点
运动,到点![]() 停止,过点
停止,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,把
,把![]() 绕点
绕点![]() 逆时针方向旋转得到
逆时针方向旋转得到 ![]() ,点
,点![]() 落在线段
落在线段![]() 上,设点
上,设点![]() 的运动时间为
的运动时间为![]() (秒)
(秒)
(1)求![]() 的长,(用含
的长,(用含![]() 的代数式表示)
的代数式表示)
(2)求点![]() 在
在![]() 的平分线上时
的平分线上时![]() 的长
的长
(3)设![]() 与
与![]() 重合部分图形的周长为
重合部分图形的周长为![]() ,当点
,当点![]() 与点
与点![]() 、
、![]() 均不重合时,求
均不重合时,求![]() 与
与![]() 之间的函数关系
之间的函数关系
(4)在点![]() 运动的同时,点
运动的同时,点![]() 从点
从点![]() 出发,以每秒9个单位长度的速度沿折线
出发,以每秒9个单位长度的速度沿折线![]() 运动,当点
运动,当点![]() 停止运动时,点
停止运动时,点![]() 也随之停止,直接写出点
也随之停止,直接写出点![]() 在直线
在直线![]() 上时
上时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在⊙O中,BC=2,AB=AC,点D为AC上的动点,且cosB=![]() .
.
(1)求AB的长度;
(2)求ADAE的值;
(3)过A点作AH⊥BD,求证:BH=CD+DH.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com