
【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

【答案】见解析
【解析】
(1)根据四边形ABCD是平行四边形,由平行四边形的性质可得:![]() ,
,![]() ,
,
根据![]() ,利用平行四边形的判定定理可得:四边形AECF是平行四边形,
,利用平行四边形的判定定理可得:四边形AECF是平行四边形,
![]() 由
由![]() 得四边形AECF是平行四边形,根据平行四边形的性质可得:
得四边形AECF是平行四边形,根据平行四边形的性质可得:![]() ,
,
根据![]() ,
,![]() ,
,![]() ,可得:
,可得:![]() ,
,![]() ,根据平行四边形的判定定理可得:四边形BFDE是平行四边形,再根据平行四边形的性质可得:
,根据平行四边形的判定定理可得:四边形BFDE是平行四边形,再根据平行四边形的性质可得:![]() ,根据平行四边形的判定定理可得:四边形EGFH是平行四边形,由平行四边形的性质可得:
,根据平行四边形的判定定理可得:四边形EGFH是平行四边形,由平行四边形的性质可得:
![]() 与GH互相平分.
与GH互相平分.
![]() 四边形ABCD是平行四边形,
四边形ABCD是平行四边形,
![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形AECF是平行四边形,
四边形AECF是平行四边形,
![]() 由
由![]() 得:四边形AECF是平行四边形,
得:四边形AECF是平行四边形,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形BFDE是平行四边形,
四边形BFDE是平行四边形,
![]() ,
,
![]() 四边形EGFH是平行四边形,
四边形EGFH是平行四边形,
![]() 与GH互相平分.
与GH互相平分.


科目:初中数学 来源: 题型:
【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车.经市场调查得知,购买6辆男式单车与8辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16 000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单车比女式单车多5辆,两种单车至少需要22辆,购置两种单车的费用不超过50 000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,MN是⊙O的切线,B为切点,BC是⊙O的弦且∠CBN=45°,过C的直线与⊙O,MN分别交于A,D两点,过C作CE⊥BD于点E.、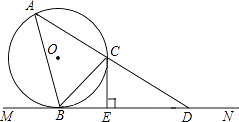
(1)求证:CE是⊙O的切线;
(2)若∠D=30°,BD=4,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在乘法公式的学习中,我们采用了构造几何图形的方法研究问题,借助直观、形象的几何模型,加深对乘法公式的认识和理解,从中感悟数形结合的思想方法,感悟几何与代数内在的统一性,根据课堂学习的经验,解决下列问题:
(1)如图①边长为(x+3)的正方形纸片,剪去一个边长为x的正方形之后,剩余部分可拼剪成一个长方形(不重叠无缝隙),则这个长方形的面积为 (用含x的式子表示).
(2)如果你有5张边长为a的正方形纸,4张长、宽分别为a、b(a>b)的长方形纸片,3张边长为b正方形纸片.现从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(不重叠无缝隙),则拼成的正方形的边长最长可以为
A.a+b;B.a+2b;C.a+3b;D.2a+b.
(3)1个大正方形和4个大小完全相同的小正方形按图②③两种方式摆放,求图③中,大正方形中未被4个小正方形覆盖部分的面积.(用含m、n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,已知点A(-5,0),B(5,0),D(2,7).
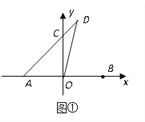
(1)若点C为AD与y轴的交点,求C点的坐标;【提示:设C点的坐标为(0,x)】
(2)动点P从B点出发以每秒1个单位的速度沿BA方向运动,同时动点Q从C点出发,也以每秒1个单位的速度沿y轴正半轴方向运动.(当P点运动到A点时,两点都停止运动,如图②所示).设从出发起运动了x秒.
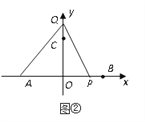
①请用含x的代数式分别表示P、Q两点的坐标;
②当x=2时,y轴上是否存在一点E,使得△AQE的面积与△APQ的面积相等?若存在,求E点的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A.平均数为160
B.中位数为158
C.众数为158
D.方差为20.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com