
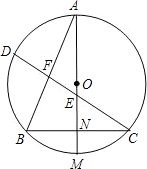
 如图,AM是⊙O的直径,过⊙O上一点B作BN⊥AM,垂足为N,其延长线交⊙O于点C,弦CD交AM于点E.
如图,AM是⊙O的直径,过⊙O上一点B作BN⊥AM,垂足为N,其延长线交⊙O于点C,弦CD交AM于点E.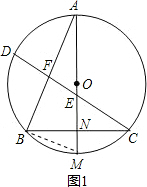 (1)证明:如图1,连接BM,
(1)证明:如图1,连接BM,
 |
| ADB |
 |
| DBC |
 |
| AD |
 |
| BC |
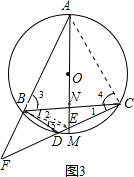 .
.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
 如图,直y=mx与双曲线y=
如图,直y=mx与双曲线y=| k |
| x |
| A、1 | B、m-1 | C、2 | D、m |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•天津)“三等分任意角”是数学史上一个著名问题.已知一个角∠MAN,设∠α=
(2012•天津)“三等分任意角”是数学史上一个著名问题.已知一个角∠MAN,设∠α=| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044

(1)若每层楼高HF为3.6m,则每层楼应设多少级阶梯?楼宽EF是多少?楼梯ACB的直扶手有多长?
(2)若每层楼有22级阶梯,则6层的平顶楼有多高、多宽?
(3)楼梯的倾斜角是多少?
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-反比例函数的性质、k的几何意义(带解析) 题型:单选题
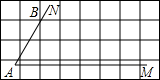
如图,直y=mx与双曲线y= 交于点A,B.过点A作AM⊥x轴,垂足为点M,连接BM.若S△ABM=1,则k的值是( )
交于点A,B.过点A作AM⊥x轴,垂足为点M,连接BM.若S△ABM=1,则k的值是( )
A. 1 B. m﹣1 C. 2 D. m
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-反比例函数的性质、k的几何意义(解析版) 题型:选择题
如图,直y=mx与双曲线y= 交于点A,B.过点A作AM⊥x轴,垂足为点M,连接BM.若S△ABM=1,则k的值是( )
交于点A,B.过点A作AM⊥x轴,垂足为点M,连接BM.若S△ABM=1,则k的值是( )

A. 1 B. m﹣1 C. 2 D. m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com