
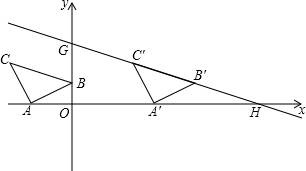
| k |
| x |
| 6 |
| x |
|
| k |
| x |
| k |
| x |
| 6 |
| x |
|
| 1 |
| 3 |
| 1 |
| 3 |
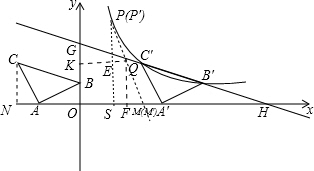
| 3 |
| 2 |
| 5 |
| 2 |
| 6 |
| x |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 6 |
| x |
| 6 | ||
|
| 12 |
| 3-2t |
| 3 |
| 2 |
| 12 |
| 3-2t |
| 5 |
| 2 |
| 12 |
| 3-2t |
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 10 |
| 3 |
| 2 |
| 6 |
| 5 |
| 12 |
| 3-2t |
| 3 |
| 2 |
| 9 |
| 5 |
| 6 |
| 5 |
| 9 |
| 5 |


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A��-3 | B��-19 | C��19 | D��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 �߹���ͼ����д������������ͼ�ۼ���
�߹���ͼ����д������������ͼ�ۼ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 СС����˿ñ���ճ�������ȴ���źܴ�����ã����õ���˿ñ��������˿���Ľ���ñ����Ƚ�һ�£�����ͬ����ȺͿ��ȣ�ָƽ�б�ľ��룩����������ñ������ͼ�������������٣�������ñë�����ϵı����Ƕ��٣�
СС����˿ñ���ճ�������ȴ���źܴ�����ã����õ���˿ñ��������˿���Ľ���ñ����Ƚ�һ�£�����ͬ����ȺͿ��ȣ�ָƽ�б�ľ��룩����������ñ������ͼ�������������٣�������ñë�����ϵı����Ƕ��٣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
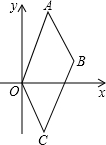 ��ͼ����ƽ��ֱ������ϵ�У�A��1��3����B��2��1�����ı���ABCD��ƽ���ı��Σ����C�����꣮
��ͼ����ƽ��ֱ������ϵ�У�A��1��3����B��2��1�����ı���ABCD��ƽ���ı��Σ����C�����꣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 �ñ߳�Ϊ1��������ֽƬ������һ�����ɰ壬����ƴ����ͼ�ġ�С��족������Ӱ���ֵ������ԭ�����������
�ñ߳�Ϊ1��������ֽƬ������һ�����ɰ壬����ƴ����ͼ�ġ�С��족������Ӱ���ֵ������ԭ������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
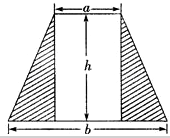 ��1���ô���ʽ��ʾͼ����Ӱ���ֵ����S��
��1���ô���ʽ��ʾͼ����Ӱ���ֵ����S���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com