
分析 (1)在y=-$\frac{1}{3}$x+1中,令x=0,则y=1,令y=0,则x=3,得到A(0,1),C(3,0),于是得到结论;
(2)由点F为线段BC的中点,得到F(3,$\frac{1}{2}$),作B关于直线y=x的对称点B′,得到B′(1,3),作F关于x轴的对称点F′,则F′(3,-$\frac{1}{2}$),连接B′F′交l2与P,交x轴于Q,则此时四边形BFQP的周长最小,求得直线B′F′的解析式为:y=-$\frac{7}{4}$x+$\frac{19}{4}$,列方程组得到P($\frac{19}{11}$,$\frac{19}{11}$),作B′G∥y轴,F′G∥x轴,两线交于G,根据勾股定理得到结论;
(3)①如图2,若OM=MN,过N作NI⊥x轴于I,根据等腰三角形的性质得到∠ACO=∠DCO,根据相似三角形的判定和性质得到NI:IC:CN=1:3:$\sqrt{10}$,设NI=m,CI=3m,CN=$\sqrt{10}$m,得到OM=MN=$\sqrt{10}$m,MI=IC=3m,列方程得到N($\frac{24+9\sqrt{10}}{26}$,-$\frac{18-3\sqrt{10}}{26}$);
②如图3,当OM=ON,过N作NI⊥x轴于I,则△CMN是等腰三角形,设IN=m,根据勾股定理得到N($\frac{12}{13}$,-$\frac{9}{13}$);③如图4,当OM=MN,过N作NI⊥x轴于I,则△CMN是等腰三角形,设IN=m,同①得,IN=m,IC=IM=3m,CN=$\sqrt{10}$m列方程得到N($\frac{24-9\sqrt{10}}{26}$,-$\frac{18+3\sqrt{10}}{26}$).
解答 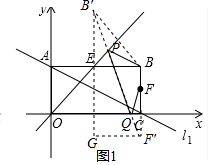 解:(1)在y=-$\frac{1}{3}$x+1中,令x=0,则y=1,令y=0,则x=3,
解:(1)在y=-$\frac{1}{3}$x+1中,令x=0,则y=1,令y=0,则x=3,
∴A(0,1),C(3,0),
∴OA=1,OC=3,
∵四边形ABCO是矩形,
∴B(3,1),
∵直线l2:y=x交线段AB于点E,
∴E(1,1);
(2)∵点F为线段BC的中点,
∴F(3,$\frac{1}{2}$),
作B关于直线y=x的对称点B′,
则△B′EB是等腰直角三角形,
∴B′(1,3),
作F关于x轴的对称点F′,则F′(3,-$\frac{1}{2}$),连接B′F′交l2与P,交x轴于Q,
则此时四边形BFQP的周长最小,
∵B′(1,3),F′(3,-$\frac{1}{2}$),
∴直线B′F′的解析式为:y=-$\frac{7}{4}$x+$\frac{19}{4}$,
解$\left\{\begin{array}{l}{y=x}\\{y=-\frac{7}{4}x+\frac{19}{4}}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{19}{11}}\\{y=\frac{19}{11}}\end{array}\right.$,
∴P($\frac{19}{11}$,$\frac{19}{11}$),
作B′G∥y轴,F′G∥x轴,两线交于G,
则B′G=$\frac{7}{2}$,GF′=2,
∴B′F′=$\sqrt{(\frac{7}{2})^{2}+{2}^{2}}$=$\frac{\sqrt{65}}{2}$,
∴四边形BFQP周长的最小值是$\frac{\sqrt{65}}{2}$+$\frac{1}{2}$;
(3)存在,
①如图2,若OM=MN,
过N作NI⊥x轴于I,
∵AO=OD,OC⊥AD,
∴AC=CD,
∴∠ACO=∠DCO,
∵l3∥l1,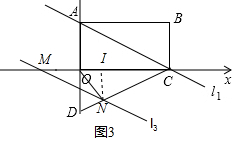
∴∠CMN=∠ACO,
∴∠ODC=∠CMN,
∴MN=CN,
∵△CIN∽△COD,
∴NI:IC:CN=1:3:$\sqrt{10}$,
设NI=m,CI=3m,CN=$\sqrt{10}$m,
∴OM=MN=$\sqrt{10}$m,MI=IC=3m,
∴$\sqrt{10}$m+3m+3m=3,
∴m=$\frac{18-3\sqrt{10}}{26}$=IN,
∴OI=($\sqrt{10}$+3)•m=$\frac{24+9\sqrt{10}}{26}$,
∴N($\frac{24+9\sqrt{10}}{26}$,-$\frac{18-3\sqrt{10}}{26}$);
②如图3,当OM=ON,
过N作NI⊥x轴于I,则△CMN是等腰三角形,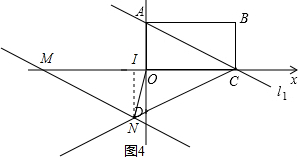
∴MN=NC,设IN=m,
同①得,IN=m,IC=IM=3m,CN=$\sqrt{10}$m,
∴OM=6m-3,
∴ON=6m-3,OI=OC-IC=3-3m,
在Rt△OIN中,(6m-3)2=m2+(3-3m)2,
∴m=$\frac{9}{13}$,m=0(舍去),
∴OI=3-3×$\frac{9}{13}$=$\frac{12}{13}$,
∴N($\frac{12}{13}$,-$\frac{9}{13}$);
③如图4,当OM=MN,
过N作NI⊥x轴于I,则△CMN是等腰三角形,
∴MN=NC,设IN=m,
同①得,IN=m,IC=IM=3m,CN=$\sqrt{10}$m,
∴OM=MN=CN=$\sqrt{10}$m=6m-3,
∴m=$\frac{18+3\sqrt{10}}{26}$,
∴OI=CI-3=3m-3=$\frac{-24+9\sqrt{10}}{26}$,
∴N($\frac{24-9\sqrt{10}}{26}$,-$\frac{18+3\sqrt{10}}{26}$);
综上所述:点N的坐标是($\frac{24+9\sqrt{10}}{26}$,-$\frac{18-3\sqrt{10}}{26}$),($\frac{12}{13}$,-$\frac{9}{13}$),($\frac{24-9\sqrt{10}}{26}$,-$\frac{18+3\sqrt{10}}{26}$).
点评 本题考查了一次函数图象上点的坐标特征,矩形的性质,等腰三角形的性质,相似三角形的判定和性质,勾股定理,轴对称的性质,正确的作出图形是解题的关键.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:选择题
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$(秒) | 30 | 30 | 28 | 28 |
| S2 | 1.21 | 1.05 | 1.21 | 1.05 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相等的角是对顶角 | |
| B. | 平行于同一条直线的两条直线互相平行 | |
| C. | 同旁内角互补 | |
| D. | 垂直于同一条直线的两条直线互相垂直 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
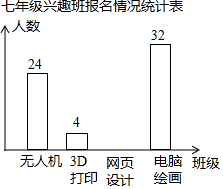 学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页打印”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名,根据报名的情况绘制了下面统计图,请回答问题.
学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页打印”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名,根据报名的情况绘制了下面统计图,请回答问题.| 兴趣班名称 | 频率 |
| “无人机” | a |
| “3D打印” | b |
| “网页设计” | 0.25 |
| “电脑绘画” | 0.4 |
| 合计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com