
【题目】关于反比例函数y= ![]() 的图象,下列说法正确的是( )
的图象,下列说法正确的是( )
A.图象经过点(1,1)
B.两个分支分布在第二、四象限
C.两个分支关于x轴成轴对称
D.当x<0时,y随x的增大而减小
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列关于函数y= ![]() (x﹣6)2+3的图象,下列叙述错误的是( )
(x﹣6)2+3的图象,下列叙述错误的是( )
A.图象是抛物线,开口向上
B.对称轴为直线x=6
C.顶点是图象的最高点,坐标为(6,3)
D.当x<6时,y随x的增大而减小;当x>6时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专买店销售A,B两种型号的新能源汽车,上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的件价各为多少万元;
每辆A型车和B型车的售价分别是x万元,y万元.
根据题意,列方程组
解这个方程组,得x= ,y=
答: .
(2)有一家公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不超过130万元,求这次购进B型车最多几辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简![]() ÷(
÷(![]() -
-![]() ),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值
),然后再从-2<x≤2的范围内选取一个合适的x的整数值代入求值
【答案】4.
【解析】试题分析:先将原分式进行化解,化解过程中注意不为0的量,根据不为0的量结合x的取值范围得出合适的x的值,将其代入化简后的代数式中即可得出结论.
试题解析:原式=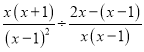 =
=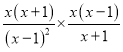 =
=![]() .
.
其中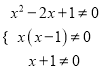 ,即x≠﹣1、0、1.
,即x≠﹣1、0、1.
又∵﹣2<x≤2且x为整数,∴x=2.
将x=2代入![]() 中得:
中得: ![]() =
=![]() =4.
=4.
考点:分式的化简求值.
【题型】解答题
【结束】
21
【题目】解方程:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(﹣2,0),C(2,2),过C作CB⊥x轴于B.
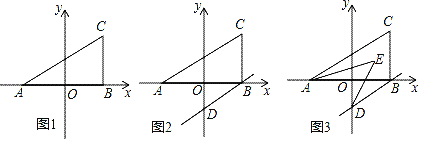
(1)如图1,△ABC的面积是 ;
(2)如图1,在y轴上找一点P,使得△ABP的面积与△ABC的面积相等,请直接写出P点坐标: ;
(3)如图2,若过B作BD∥AC交y轴于D,则∠BAC+∠ODB的度数为 度;
(4)如图3,BD∥AC,若AE、DE分别平分∠CAB,∠ODB,求∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E是BC的中点,连接并延长DE交AB的延长线于点F. 
(1)求证:△CDE≌△BFE;
(2)若CD=3cm,请求出AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点![]() ,
,![]() ,
,![]() ,a是
,a是![]() 的立方根,方程
的立方根,方程![]() 是关于x,y的二元一次方程,d为不等式组
是关于x,y的二元一次方程,d为不等式组![]() 的最大整数解.
的最大整数解.
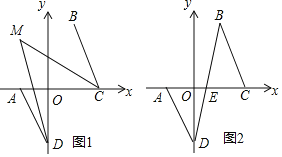
![]() 求点A、B、C的坐标;
求点A、B、C的坐标;
![]() 如图1,若D为y轴负半轴上的一个动点,当
如图1,若D为y轴负半轴上的一个动点,当![]() 时,
时,![]() 与
与![]() 的平分线交于M点,求
的平分线交于M点,求![]() 的度数;
的度数;
![]() 如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使
如图2,若D为y轴负半轴上的一个动点,连BD交x轴于点E,问是否存在点D,使![]() ?若存在,请求出D的纵坐标
?若存在,请求出D的纵坐标![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出它关于原点的对称点称为一次变换,已知点A的坐标为(﹣2,0),把点A经过连续2014次这样的变换得到的点A2014的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
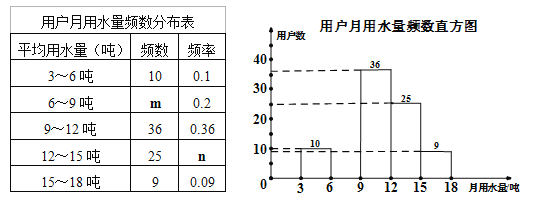
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m= ,n= ;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com