
【题目】如图,已知AC=BC,点D是BC上一点,∠ADE=∠C.
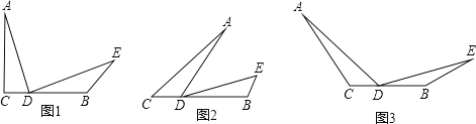
(1)如图1,若∠C=90°,∠DBE=135°.
①求证:∠EDB=∠CAD;
②求证:DA=DE;
(2)如图2,若∠C=40°,DA=DE,求∠DBE的度数;
(3)如图3,请直接写出∠DBE与∠C之间满足什么数量关系时,总有DA=DE成立.
【答案】(1)①证明见解析;②证明见解析;(2)∠AGD=110°;(3)∠DBE=90°+![]() ∠C.
∠C.
【解析】
(1)①根据三角形的内角和及平角的定义可得结论;
②如图1,作辅助线,构建等腰直角三角形,利用ASA证明△AFD≌△DBE(ASA),可得结论;
(2)方法一:如图2,同理作辅助线,证明△AGD≌△DBE(SAS),得∠AGD=∠DBE=110°;
方法二:如图2,延长DB到点H使DH=AC,连接EH,证明△ACD≌△DHE(SAS),得∠C=∠H=40°,CD=EH,再根据已知证明CD=BH=EH,可得结论;
(3)同理作辅助线,证明△AFD≌△DBE(SAS),根据三角形的外角和三角形内角和定理可得结论.
(1)证明:①∵∠ADE=∠C,
∴∠CAD=180°-∠C-∠ADC,
∠EDB=180°-∠ADE-∠ADC,
∴∠CAD=∠EDB;
②在AC上截取CF=CD,连接FD,(或在AC上截取AF=BD,连接FD)
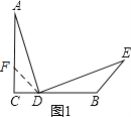
∵∠C=90°,
∴∠CFD=∠CDF=45°,
∴∠AFD=135°=∠DBE,
∵AC=BC,
∴AC-CF=BC-CD,即:AF=BD,
由①知:∠CAD=∠BDE,
∴△AFD≌△DBE(ASA),
∴DA=DE;
(2)方法一:如图2,在AC上截取AG=DB,连接GD(在AC上截取CG=CD,连接GD),
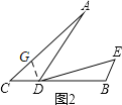
∵AC=BC,
∴AC-AG=BC-BD即:CG=CD,
∴∠CGD=∠CDG=![]() =70°,
=70°,
∵DA=DE,∠CAD=∠EDB(已证),AG=DB,
∴△AGD≌△DBE(SAS),
∴∠AGD=∠DBE=110°;
方法二:如图3,延长DB到点H使DH=AC,连接EH,

∵∠CAD=∠BDE,AD=DE,
∴△ACD≌△DHE(SAS),
∴∠C=∠H=40°,CD=EH,
∵AC=BC=DH,
∴CD=BH=EH,
∴∠HBE=∠HEB=70°,
∴∠DBE=110°;
(3)当∠DBE=90°+![]() ∠C时,总有DA=DE成立;
∠C时,总有DA=DE成立;
理由是:如图3,在AC上截取CF=CD,连接DF,则∠CDF=∠CFD,
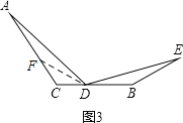
设∠CDF=x,
△CDF中,∠C+∠CDF+∠CFD=180°,
∴∠C+x+x=180°,
x=![]() =90°-
=90°-![]() ,
,
同理得△AFD≌△DBE(SAS),
∴∠AFD=∠DBE=∠C+∠CDF=∠C+x=∠C+90°-![]() ∠C,
∠C,
∴∠DBE=90°+![]() ∠C.
∠C.


科目:初中数学 来源: 题型:
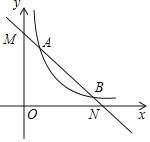
【题目】如图,在平面直角坐标中,点O是坐标原点,一次函数y1=﹣x+4与反比例函数y2=![]() (x>0)的图象交于A(1,m)、B(n,1)两点.
(x>0)的图象交于A(1,m)、B(n,1)两点.
(1)求k、m、n的值.
(2)根据图象写出当y1>y2时,x的取值范围.
(3)若一次函数图象与x轴、y轴分别交于点N、M,则求出△AON的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
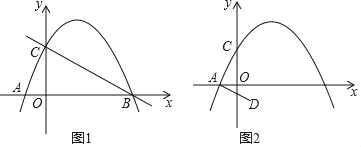
【题目】已知:抛物线y=﹣![]() x2+bx+c交x轴于点A(﹣1,0)和点B,交y轴于点C(0,2)
x2+bx+c交x轴于点A(﹣1,0)和点B,交y轴于点C(0,2)
(1)求抛物线的表达式;
(2)点P为第一象限抛物线上一点,是否存在使△PBC面积最大的点P?若不存在,请说明理由;若存在,求出点P的坐标;
(3)点D坐标为(1,﹣1),连接AD,将线段AD绕平面内某一点旋转180度得线段MN(点M、N分别与点A、D对应),使点M、N都在抛物线上,求点M、N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠CAB=∠DAB下列条件中不能使△ABC≌△ABD的是( )
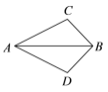
A. ∠C=∠D B. ∠ABC=∠ABD C. AC=AD D. BC=BD
查看答案和解析>>
科目:初中数学 来源: 题型:
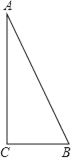
【题目】如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李刚和父母一起从家到姑妈家去,两地相距![]() ,出发前汽车油箱里有
,出发前汽车油箱里有![]() 油,途中加油若干升,加油前后汽车都以
油,途中加油若干升,加油前后汽车都以![]() 的速度匀速行驶.已知油箱中剩余油量
的速度匀速行驶.已知油箱中剩余油量![]() 与行驶时间
与行驶时间![]() 之间的关系如图所示.则下列说法:①汽车行驶了
之间的关系如图所示.则下列说法:①汽车行驶了![]() 后加油;②途中加油
后加油;②途中加油![]() ;③加油前油箱中剩余油量
;③加油前油箱中剩余油量![]() 与行驶时间
与行驶时间![]() 之间的函数关系式是
之间的函数关系式是![]() ;④汽车加油后还可行驶
;④汽车加油后还可行驶![]() ;⑤汽车到达姑妈家,油箱中还剩余
;⑤汽车到达姑妈家,油箱中还剩余![]() 油.其中全部正确的是( )
油.其中全部正确的是( )
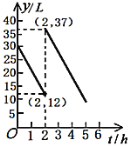
A.①④⑤B.①③④C.②⑤D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
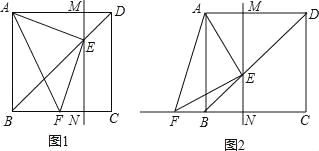
【题目】如图,点 E 是边长为 1 的正方形 ABCD 的对角线 BD 上的一个动点(不与 B、D 两点重合),过点 E 作直线 MN∥DC,交 AD 于 M,交 BC 于 N,连接 AE,作 EF⊥AE 于 E,交直线 CB 于 F.
(1)如图 1,当点 F 在线段 CB 上时,通过观察或测量,猜想△AEF 的形状,并证明你的猜想;
(2)如图 2,当点 F 在线段 CB 的延长线上时,其它条件不变,(1)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由;
(3)在点 E 从点D 向点B 的运动过程中,四边形 AFNM 的面积是否会发生变化?若发生了变化,请说明理由;若没有发生变化,请求出其面积的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
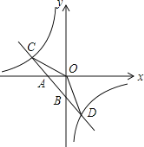
【题目】如图,已知一次函数![]() 的图象与x轴、y轴分别交于A、B两点,与反比例函数
的图象与x轴、y轴分别交于A、B两点,与反比例函数![]() 的图象分别交于C、D两点,点D(2,﹣3),点A(-2,0).
的图象分别交于C、D两点,点D(2,﹣3),点A(-2,0).
(1)求一次函数![]() 与反比例函数
与反比例函数![]() 的解析式;
的解析式;
(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示在三角形△ABC中AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E、F,则下列四个结论中,①AB上一点与AC上一点到D的距离相等;②AD上任意一点到AB、AC的距离相等;③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的个数是
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com