
分析 (1)利用题意计算进而求出答案;
(2)①利用已知得出关于a,b的等式求出答案;
②根据题意列不等式组即可得到结论;
③根据题意列方程和不等式组即可得到结论.
解答 解:(1)∵L(x,y)=x+3y,
∴L(2,1)=2+3×1=5,L($\frac{3}{2}$,$\frac{1}{2}$)=$\frac{3}{2}$+$\frac{1}{2}×$3=3,
故答案为:5,3;
(2)①∵L(x,y)=ax+by,L(1,-2)=-1,L($\frac{1}{3}$,$\frac{1}{2}$)=2,
∴$\left\{\begin{array}{l}{a-2b=-1}\\{\frac{1}{3}a+\frac{1}{2}b=2}\end{array}\right.$,∴$\left\{\begin{array}{l}{a=3}\\{b=2}\end{array}\right.$,
故答案为:3,2;
②由(2)知,L(m,m-2)=3m+2(m-2)=5m-4,
∵50<L(m,m-2)<100,
∴$\left\{\begin{array}{l}{5m-4>50}\\{5m-4<100}\end{array}\right.$,
解得:$\frac{54}{5}$<m<$\frac{104}{5}$,
∵m和m-2均为为正整数,
∴满足50<L(m,m-2)<100的正格数对有10个;
③由L(x,y)=3x+2y=76得y=$\frac{76-3x}{2}$,
∵x>0,y>0,即$\frac{76-3x}{2}$>0,
∴0<x<25$\frac{1}{3}$,
∵x,y均为为正整数,
∴x为偶数,
∴共有12个满足这样的正格数,
若x,y满足②,则x-y=2,即x-$\frac{76-3x}{2}$=2,
解得:x=16,
∴y=x-2=14,
∴在这些正格数对中,有满足问题②的数对,为$\left\{\begin{array}{l}{x=16}\\{y=14}\end{array}\right.$.
点评 此题主要考查了一元一次不等式的应用,二元一次方程组的应用,以及新定义,根据题意得出正确等式是解题关键.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
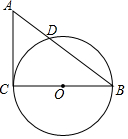 如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O,交AB于点D.
如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O,交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com