
分析 由m、n满足3m2-7m+1=0,n2-7n+3=0,结合求根公式即可得出m、n的值,再由mn≠1,可得出m、n的值里面同+或同-,将m、n的值代入m-$\frac{m-1}{n}$中即可得出结论.
解答 解:∵m、n满足3m2-7m+1=0,n2-7n+3=0,
∴m=$\frac{7±\sqrt{37}}{6}$,n=$\frac{7±\sqrt{37}}{2}$.
又∵mn≠1,
∴$\left\{\begin{array}{l}{m=\frac{7+\sqrt{37}}{6}}\\{n=\frac{7+\sqrt{37}}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{m=\frac{7-\sqrt{37}}{6}}\\{n=\frac{7-\sqrt{37}}{2}}\end{array}\right.$.
当$\left\{\begin{array}{l}{m=\frac{7+\sqrt{37}}{6}}\\{n=\frac{7+\sqrt{37}}{2}}\end{array}\right.$时,m-$\frac{m-1}{n}$=$\frac{7+\sqrt{37}}{6}$-$\frac{1}{3}$+$\frac{2}{7+\sqrt{37}}$=$\frac{7+\sqrt{37}}{6}$-$\frac{1}{3}$+$\frac{7-\sqrt{37}}{6}$=2;
当$\left\{\begin{array}{l}{m=\frac{7-\sqrt{37}}{6}}\\{n=\frac{7-\sqrt{37}}{2}}\end{array}\right.$时,m-$\frac{m-1}{n}$=$\frac{7-\sqrt{37}}{6}$-$\frac{1}{3}$+$\frac{2}{7-\sqrt{37}}$=$\frac{7-\sqrt{37}}{6}$-$\frac{1}{3}$+$\frac{7+\sqrt{37}}{6}$=2.
综上可知:m-$\frac{m-1}{n}$=2.
故答案为:2.
点评 本题考查了求根公式以及分式的化解求值,解题的关键是求出m、n的值.本题属于基础题,难度不大,解决该题型题目时,根据求根公式得出m、n的值是关键.


科目:初中数学 来源:2016-2017学年新疆乌鲁木齐市八年级下学期第一次月考数学试卷(解析版) 题型:填空题
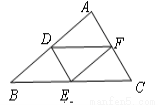
如图,D,E,F分别为△ABC三边的中点,△ABC的周长是18cm,则△DEF的周长是________cm.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省八年级3月月考数学试卷(解析版) 题型:单选题
用配方法将方程x2+6x-11=0变形为( )
A. (x-3)2=20 B. (x+3)2=20 C. (x+3)2=2 D. (x-3)2=2
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
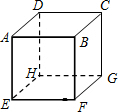 用大小相同、表面均为白色或红色的若干个小正方体拼接成如图所示的一个大正方体ABCD-EFGH.若大正方体的对角线AG、BH、CE、DF上所用的小正方体是表面均为红色的,而且共用了41个,大正方体其余部分用的都是表面均为白色的小正方体.则所用表面均为白色的小正方体共( )个.
用大小相同、表面均为白色或红色的若干个小正方体拼接成如图所示的一个大正方体ABCD-EFGH.若大正方体的对角线AG、BH、CE、DF上所用的小正方体是表面均为红色的,而且共用了41个,大正方体其余部分用的都是表面均为白色的小正方体.则所用表面均为白色的小正方体共( )个.| A. | 688 | B. | 959 | C. | 1290 | D. | 1687 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\frac{a}{b}$)2=$\frac{{a}^{2}}{b}$ | B. | $\frac{1}{a}+\frac{1}{b}=\frac{2}{a+b}$ | C. | $\frac{{x}^{2}-{y}^{2}}{x-y}=x+y$ | D. | $\frac{-x-y}{x-y}=-1$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com