
 某校中考模拟试题中有这样一道试题:
某校中考模拟试题中有这样一道试题:分析 (1)在B点选择右拐的可能性为$\frac{1}{2}$,在D点选择左拐的可能性为$\frac{1}{2}$,根据乘法原理即可得出结论;
(2)同(1)的道理,找出吃到树叶2的概率,由事件的独立性利用加法原理即可解决问题;
(3)按照做题过程分析写明理由即可;
(4)根据新课标以及概率这一章节的教学目标分析该道试题,即可得出结论.
解答 解:(1)根据乘法原理,得p=$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{4}$=25%,
∴吃到树叶1的概率为25%.
(2)根据乘法原理,得p=$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{4}$=25%,
∴吃到树叶2的概率为25%.
根据加法原理,得p=25%+25%=50%,
∴吃到树叶的概率为50%.
(3)在解决(1)时,在B点选择右拐的可能性为$\frac{1}{2}$,在D点选择左拐的可能性为$\frac{1}{2}$,
根据乘法原理即可解决(1);
在解决(2)时,首先要明白吃到树叶包括树叶1和树叶2,接下来要找出吃到树叶2的概率,
同理可得出吃到树叶2的概率为25%,
根据概率事件的加法原理即可解决(2).
(3)不恰当.理由:
①课程标准和考试要求中概率的教学要求只是“了解”和“计算简单事件的概率”;
②初中阶段概率的计算仅限于“机会均等”的情况;
③题中E枝上的三枝花容易误导学生,使计算错误.
点评 本题考查了概率事件的加法原理和乘法原理,解题的关键是:(1)分析吃到树叶1的路径;(2)根据加法原理得出结论;(3)按照做题过程分析理由;(4)按教学目标来分析该题.本题属于中档题,难度不大,解决该题型题目时,分析完成事件的步骤得出概率是关键.


 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:选择题
| A. | m≥0 | B. | m≤0 | C. | m≠1 | D. | m≤0且m≠-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
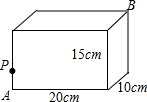 如图,长方体的长为20cm,宽为10cm,高为15cm,棱上点P与顶点A相距5cm,一只蚂蚁如果要沿着长方体表面从点P爬到点B处,需要爬行的最短距离是多少?
如图,长方体的长为20cm,宽为10cm,高为15cm,棱上点P与顶点A相距5cm,一只蚂蚁如果要沿着长方体表面从点P爬到点B处,需要爬行的最短距离是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
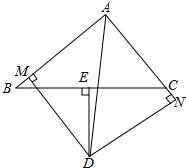 如图,△ABC中,E是BC边上的中点,DE⊥BC于E,交∠BAC的平分线AD于D,过D点作DM⊥AB于M,作DN⊥AC于N,试证明:BM=CN.
如图,△ABC中,E是BC边上的中点,DE⊥BC于E,交∠BAC的平分线AD于D,过D点作DM⊥AB于M,作DN⊥AC于N,试证明:BM=CN.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
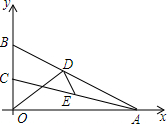 如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )
如图,在平面直角坐标系xOy中,已知点A(8,0),点B、C在y轴的正半轴上,且∠ABO=70°,∠ACO=80°,点D、E分别是线段AB、AC上的动点,则线段OD+DE的最小值等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<0 | B. | x<$\frac{1}{2}$ | C. | x$≥\frac{1}{2}$ | D. | x$>\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,E、F、G分别是BC、AB、AC上一点,∠FEG=2∠B.
如图,△ABC中,AB=AC,E、F、G分别是BC、AB、AC上一点,∠FEG=2∠B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com