
【题目】如图,矩形![]() 的顶点A、C分别在
的顶点A、C分别在![]() 、
、![]() 的正半轴上,反比例函数
的正半轴上,反比例函数![]() (
(![]() )与矩形
)与矩形![]() 的边AB、BC交于点D、E.
的边AB、BC交于点D、E.

(1)若![]() ,则
,则![]() 的面积为_________;
的面积为_________;
(2)若D为AB边中点.
①求证:E为BC边中点;
②若![]() 的面积为4,求
的面积为4,求![]() 的值.
的值.
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1.
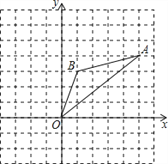
(1)画出△A1OB1;
(2)求在旋转过程中线段AB、BO扫过的图形的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】常常听说“勾3股4弦5”,是什么意思呢?它就是勾股定理,即“直角三角形两直角边长a,b与斜边长c之间满足等式:a2+b2=c2”的一个最简单特例.我们把满足a2+b2=c2的三个正整数a,b,c,称为勾股数组,记为(a,b,c).
(1)请在下面的勾股数组表中写出m、n、p合适的数值:
a | b | c | a | b | c |
3 | 4 | 5 | 4 | 3 | 5 |
5 | 12 | m | 6 | 8 | 10 |
7 | 24 | 25 | p | 15 | 17 |
9 | n | 41 | 10 | 24 | 26 |
11 | 60 | 61 | 12 | 35 | 37 |
… | … | … | … | … | … |
平面直角坐标系中,横、纵坐标均为整数的点叫做整点(格点).过x轴上的整点作y轴的平行线,过y轴上的整点作x轴的平行线,组成的图形叫做正方形网格(有时简称网格),这些平行线叫做格边,当一条线段AB的两端点是格边上的点时,称为AB在格边上.顶点均在格点上的多边形叫做格点多边形.在正方形网格中,我们可以利用勾股定理研究关于图形面积、周长的问题,其中利用割补法、作图法求面积非常有趣.
(2)已知△ABC三边长度为4、13、15,请在下面的网格中画出格点△ABC并计算其面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于M,BN⊥MN于N.
(1)MN=AM+BN成立吗?为什么?
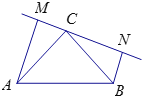
(2)若过点C在△ABC内作直线MN,AM⊥MN于M,BN⊥MN于N,则AM、BN与MN之间有什么关系?请说明理由.
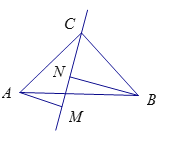
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为3厘米,点B为⊙O外一点,OB交⊙O于点A,且AB=OA,动点P从点A出发,以π厘米/秒的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为( )秒时,直线BP与⊙O相切.
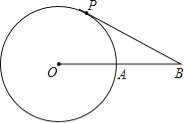
A. 1 B. 5 C. 0.5或5.5 D. 1或5
查看答案和解析>>
科目:初中数学 来源: 题型:
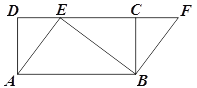
【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察下列图形与等式的关系,并填空:
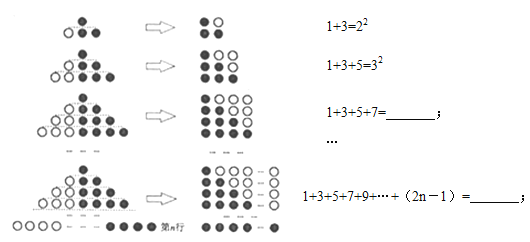
(2)利用(1)中结论,解决下列问题:
①1+3+5+…+2005= ;
②计算:101+103+105+…+199;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
-1、2、-4、8、-16、32、-64、……①
0、3、-3、9、-15、33、-63、……②
1、-5、7、-17、31、-65、127、……③
(1) 第①行的第8个数是___________,第①行第n个数是___________(用n的式子表示)
(2) 取第①、②、③行的第10个数分别记为a、b、c,求a-b+c的值
(3) 取每行数的第n个数,这三个数中任意两数之差的最大值为6146,则n=__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某班“讲故事”比赛中有一个抽奖活动,活动规则是:只有进入最后决赛的甲、乙、丙三位同学,每人才能获得一次抽奖机会.在如图所示的翻奖牌正面的4个数字中选一个数字,选中后就可以得到该数字后面的相应奖品:前面的人选中的数字,后面的人就不能再选择数字了.
(1)请用树状图(或列表)的方法求甲、乙二人得到的奖品都是计算器的概率.
(2)有的同学认为,如果甲先翻奖牌,那么他得到篮球的概率会大些,这种说法正确吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com