
分析 先提取$\frac{1}{4}$,将原式变形,再依次将分子化为:22=1×3+1,42=3×5+1,62=5×7=1…,拆项化分别化为1+$\frac{1}{1×3}$,1+$\frac{1}{3×5}$,1+$\frac{1}{5×7}$,…,同时$\frac{1}{1×3}$=$\frac{1}{2}$(1-$\frac{1}{3}$),$\frac{1}{3×5}$=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$),…,再代入化简即可得出结果.
解答 解:$\frac{{1}^{2}}{1×3}$+$\frac{{2}^{2}}{3×5}$+$\frac{{3}^{2}}{5×7}$+…+$\frac{5{0}^{2}}{99×101}$,
=$\frac{1}{4}$($\frac{{2}^{2}}{1×3}$+$\frac{{4}^{2}}{3×5}$+$\frac{{6}^{2}}{5×7}$+…+$\frac{10{0}^{2}}{99×101}$),
=$\frac{1}{4}$($\frac{1×3+1}{1×3}$+$\frac{3×5+1}{3×5}$+$\frac{5×7+1}{5×7}$+…+$\frac{99×101+1}{99×101}$),
=$\frac{1}{4}$(1+$\frac{1}{1×3}$+1+$\frac{1}{3×5}$+1+$\frac{1}{5×7}$+…+1+$\frac{1}{99×101}$),
=$\frac{1}{4}$[50+$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{99}$-$\frac{1}{101}$)],
=$\frac{1}{4}$[50+$\frac{1}{2}$(1-$\frac{1}{101}$)],
=$\frac{1}{4}$(50+$\frac{1}{2}$×$\frac{100}{101}$),
=$\frac{25}{2}$+$\frac{25}{202}$,
=$\frac{2525}{202}$+$\frac{25}{202}$,
=$\frac{1275}{101}$.
点评 此题考查了有理数的混合运算,此题需要利用简便方法将原式变形得出结论,要明确几个式子的关系:①22=1×3+1,42=3×5+1,62=5×7=1…,②$\frac{1}{1×3}$=$\frac{1}{2}$(1-$\frac{1}{3}$),$\frac{1}{3×5}$=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$),…,$\frac{1}{99×101}$=$\frac{1}{2}$($\frac{1}{99}$-$\frac{1}{101}$)抓住这些式子的特点,利用有理数法则,从而得出结果.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:解答题
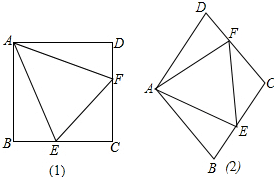 (1)如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.
(1)如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
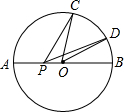 如图,已知⊙O的半径为R,C、D在直径AB的同侧半圆上,∠AOC=96°,∠BOD=36°,动点P在直径AB上,则CP+PD的最小值是( )
如图,已知⊙O的半径为R,C、D在直径AB的同侧半圆上,∠AOC=96°,∠BOD=36°,动点P在直径AB上,则CP+PD的最小值是( )| A. | 2R | B. | $\sqrt{3}$R | C. | $\sqrt{2}$R | D. | R |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com