
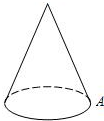
 如图,地面半径为1,母线长为4的圆锥A处有一只蚂蚁,它绕这个圆锥侧面爬行一圈后回到A处,则蚂蚁所走最短路线长为( )
如图,地面半径为1,母线长为4的圆锥A处有一只蚂蚁,它绕这个圆锥侧面爬行一圈后回到A处,则蚂蚁所走最短路线长为( )| A、2 | ||
B、4
| ||
C、4
| ||
| D、4 |
科目:初中数学 来源: 题型:
| 型号 | 速度(千米/小时) | 时间(小时) | 路程(千米) |
| 大部队 | V | 32 | |
| 突击小队 | 32 |
| 型号 | 速度(千米/小时) | 时间(小时) | 路程(千米) |
| 大部队 | t | 32 | |
| 突击小队 | 32 |
查看答案和解析>>
科目:初中数学 来源: 题型:
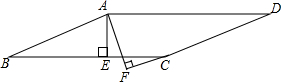 如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,S?ABCD=72,则?ABCD的周长是( )
如图所示,在?ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,S?ABCD=72,则?ABCD的周长是( )| A、64 | B、60 | C、70 | D、56 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 “三角板”是大家常见的,你思考过“三角板”中蕴含的数学问题吗?下面老师随意编一题请大家算算:
“三角板”是大家常见的,你思考过“三角板”中蕴含的数学问题吗?下面老师随意编一题请大家算算:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com