
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA(a��0)��B(b��0)����a��b����|2a+6|+(2a��3b+12)2��0����ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��2����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��
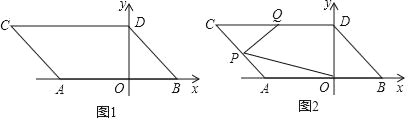
(1)��ֱ��д��A��B��C��D�ĵ�����ꣻ
(2)��ͼ2����P���߶�AC�ϵ�һ�����㣬��Q���߶�CD���е㣬����PQ��PO������P���߶�AC���ƶ�ʱ(����A��C�غ�)�����ҳ���PQD����OPQ����POB��������ϵ����֤����Ľ��ۣ�
(3)�����������Ƿ���ڵ�M��ʹ������MAD�������������ACD�������ȣ������ڣ�ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��A(��3��0)��B(2��0)��C��-5��2����D��0��2������2����PQD+��OPQ+��POB��360�������ɼ���������3��(2��0)��(��8��0)��(0����![]() )��(0��
)��(0��![]() )
)
��������
��1�����ݾ���ֵ�ķǸ��ԡ�ż�η��ķǸ��Էֱ����a��b���õ���A��B�����꣬���ɽ�����⣻
��2����������QPOBD���ڽǺͣ�����ƽ���ߵ����ʵõ���QDB����OBD��180�������㼴�ɣ�
��3���������������ACD��������ֵ�M��x���ϡ���M��y����������������������ε������ʽ���㼴�ɣ�
�⣺(1)��|2a+6|+(2a��3b+12)2��0��
��|2a+6|��0��(2a��3b+12)2��0��
��ã�a����3��b��2��
���A��B������ֱ�ΪA(��3��0)��B(2��0)��
����A��B�ֱ�����ƽ��2����λ��������ƽ��2����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D����C��-5,2��D��0,2����
(2)��PQD+��OPQ+��POB��360����
�������£������QPOBD���ڽǺͣ�(5��2)��180����540����
��CD��AB��
���QDB+��OBD��180����
���PQD+��OPQ+��POB��540����(��QDB+��OBD)��360����
(3)������ã���C������Ϊ(��5��2)����D������Ϊ(0��2)��
����ACD�������![]() ��5��2��5��
��5��2��5��
����M��x����ʱ�����M������Ϊ(x��0)��
��AM��|��3��x|��
������ã�![]() ��|��3��x|��2��5��
��|��3��x|��2��5��
��ã�x��2��8��
����M��y����ʱ�����M������Ϊ(0��y)��
��AM��|2��y|��
������ã�![]() ��|2��y|��3��5��
��|2��y|��3��5��
��ã�y����![]() ��
��![]() ��
��
����������������MAD�������������ACD��������ʱ����M������Ϊ(2��0)��(��8��0)��(0����![]() )��(0��
)��(0��![]() )��
)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y��kx��b(k��0)��ͼ���뷴��������y��![]() (m��0)��ͼ���ڵڶ����������ڵ�A��B���㣬��x�ύ��C�㣬��B���� ��Ϊ(6��n)���߶�OA��5��EΪx����һ�㣬��sin ��AOE��
(m��0)��ͼ���ڵڶ����������ڵ�A��B���㣬��x�ύ��C�㣬��B���� ��Ϊ(6��n)���߶�OA��5��EΪx����һ�㣬��sin ��AOE��![]() ��
��
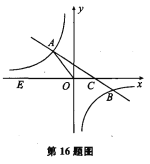
��1����÷�����������һ�κ����Ľ���ʽ
��2������AOC�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����![]() �ı߳�
�ı߳�![]() ��ijһʱ�̣�����
��ijһʱ�̣�����![]() ��
��![]() �������
�������![]() ������
������![]() ���ٶ���
���ٶ���![]() �������˶���ͬʱ������
�������˶���ͬʱ������![]() ��
��![]() �������
�������![]() ������
������![]() ���ٶ���
���ٶ���![]() �������˶����ʣ�
�������˶����ʣ�

��1����������ʱ�䣬![]() ��������ھ���
��������ھ���![]() �����
�����![]() ��
��
��2���Ƿ����ʱ��t��ʹ��A,M,NΪ�������������![]() ���ƣ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
���ƣ������ڣ���t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������ABC�ĵױ�BC��Ϊ4����AC�Ĵ�ֱƽ����EF�ֱ�AC��AB����E��F�㣮����DΪBC�ߵ��е㣬��MΪ�߶�EF��һ���㣬����CDM�ܳ�����СֵΪ8�����ABC�����Ϊ��������
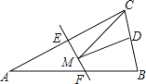
A.12B.16C.24D.32
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У������������д��������ÿλѧ����д����39�������������������鲿��ѧ������д����������Ǹ��ݳ�������Ƶ�ͳ��ͼ��һ���֣�
��� | ��ȷ����x | ���� |
A | 0��x��8 | 10 |
B | 8��x��16 | 15 |
C | 16��x��24 | 25 |
D | 24��x��32 | m |
E | 32��x��40 | n |
����������Ϣ����������⣺
��1����ͳ�Ʊ��У�m=�� ����n=�� ��������ȫ����ͳ��ͼ��
��2������ͳ��ͼ����C��������Ӧ��Բ�ĽǵĶ������� ����
��3������λ��ί��ʦ��ÿλ��ʦ��E��ѧ�����ѧУ������ʾ��ͨ����������̭�����������������������ѧУ�涨��ÿλѧ�����ٻ����λ��ί��ʦ����ͨ�������ܴ���ѧУ�μӶ�������������д����������������ͼ���E��ѧ�����ƲμӶ�������������д�������ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OA=2���Ե�AΪԲ�ģ�1Ϊ�뾶����A��OA���ӳ��߽��ڵ�C������A��OA�Ĵ��ߣ��������A��һ������ΪB������BC
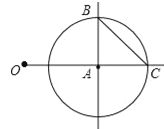
��1���߶�BC�ij����� ��
��2������ͼ�а�����Ҫ����һ���������ش����⣺
���Ե� ΪԲ�ģ����߶� �ij�Ϊ�뾶������������BA���ڵ�D��ʹ�߶�OD�ij�����![]() ��
��
����OD����OD�ϻ�����P��ʹOP�ó�����![]() ����д����������˵�����ɣ�
����д����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�Ķ��κ���y=x2����2m+3��x+m2+2
��1�������κ���y��ͼ����x�����������㣬��ʵ��m��ȡֵ��Χ��
��2������κ���y��ͼ����x��Ľ���ΪA��x1��0����B��x2��0����������x12+x22=31+|x1x2|����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ƕ���һ���µ�������![]() �������������ĸ�������
�������������ĸ�������![]() ��
��![]() ��
��![]() ��
��![]() ���������������������
���������������������![]() ��
��![]() �����ҹ涨��
�����ҹ涨��![]() .
.
���磺 ![]() .
.
���������涨����������⣺
��1�����㣺![]() ��
��
��2������������![]() ����
����![]() ��
��
��3������������![]() ����������
����������![]() ��������������
��������������![]() ��ֵ
��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2019��5��30��������¥����������ʽͨ����������Ź�ʣ�������פ��.�����Ƿ�ǰ����������������¥�������ų�Ϊ�����������.��ĩ��С���С����λͬѧ��Լǰ���ιۣ�С�������г���С�ղ��У�����ͬʱ��ѧУ��������ͬһ��·��ǰ��������һ��ʱ���С�巢�ֶ������ˣ�����������ԭ�ٷ��ص�ѧУȡ��ȡ����������������ԭ����С�ղ�����ǰ��������Ŀ�ĵغ�ȴ�С��һ��ιۣ�ȡ������ʱ����Բ��ƣ����������������˱������٣���ͼ������֮��ľ���![]() �����ʱ��
�����ʱ��![]() ֮��ĺ���ͼ����ͼ��ʾ����С�嵽��Ŀ�ĵ�ʱ��С����Ŀ�ĵػ���______��.
֮��ĺ���ͼ����ͼ��ʾ����С�嵽��Ŀ�ĵ�ʱ��С����Ŀ�ĵػ���______��.

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com