
【题目】如图,△ABC中,AD是高,BE平分∠ABC.
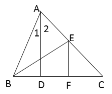
(1)若∠EBC=32°,∠1∶∠2=1∶2,EF∥AD,求∠FEC的度数.
(2)若∠2=50°,点F为射线CB上的一个动点,当△EFC为钝角三角形时,直接写出∠FEC的取值范围.
科目:初中数学 来源: 题型:
【题目】在□ABCD中,O是AC、BD的交点,过点O 与AC垂直的直线交边AD于点E,若□ABCD的周长为22cm,则△CDE的周长为( ).
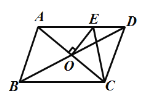
A. 8cm B. 10cm C. 11cm D. 12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为x=﹣1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).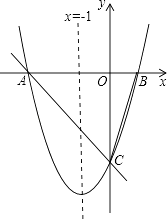
(1)求点B的坐标.
(2)已知a=1,C为抛物线与y轴的交点.
①若点P在抛物线上,且S△POC=4S△BOC , 求点P的坐标.
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先仔细阅读材料,再解决问题:
完全平方式x2±2xy+y2=(x±y)2以及(x±y)2的值为非负数的特点在数学学习中有广泛的应用,比如探求2x2+12x﹣4的最大(小)值时,我们可以配成完全平方式来解决:
解:原式=2(x2+6x﹣2)=2(x2+6x+9﹣9﹣2)=2[(x+3)2﹣11]=2(x+3)2﹣22.
∵无论x取什么数,都有(x+3)2≥0,∴(x+3)2的最小值为0;
∴x=﹣3时,2(x+3)2﹣22的最小值是2×0﹣22=﹣22;
∴当x=﹣3时,2x2+12x﹣4的最小值是﹣22.
请根据上面的解题思路,解答下列问题:
(1)多项式3x2﹣6x+12的最小值是多少,并写出对应的x的值;
(2)判断多项式![]() 有最大值还是最小值,请你说明理由并求出当x为何值时,此多项式的最大值(或最小值)是多少.
有最大值还是最小值,请你说明理由并求出当x为何值时,此多项式的最大值(或最小值)是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今年考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),你找到的密码钥匙是 ,破译“正做数学”的真实意思是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB与直线CD相交于点O,OE平分![]() .
.
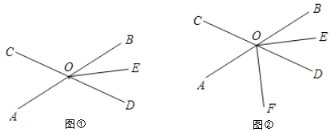
(1)如图①,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,射线OF在![]() 内部.
内部.
①若![]() ,判断OF是否为
,判断OF是否为![]() 的平分线,并说明理由;
的平分线,并说明理由;
②若OF平分![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com