
 中a的正、负不能确定,也就不能确定抛物线的开口方向,抛物线是上升还是下降也就不能确定,因此y值随x值的变化也不能确定,所以不能判断出
中a的正、负不能确定,也就不能确定抛物线的开口方向,抛物线是上升还是下降也就不能确定,因此y值随x值的变化也不能确定,所以不能判断出 和
和 的大小。
的大小。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题
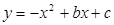 与x的两个交点分别为A(1,0),B(3,0)。
与x的两个交点分别为A(1,0),B(3,0)。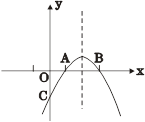
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 米.请利用下面所给的平面直角坐标系探索下列问题:
米.请利用下面所给的平面直角坐标系探索下列问题:
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与
与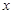 轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当
轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当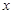 =O和
=O和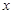 =4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
=4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。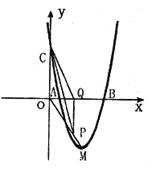
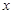 轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 、
、 ,-1,0、1、3的6张卡片,背面完全相同,洗匀后,从中任取两张,该卡片上的数分别作为点P 的横坐标和纵坐标,P落在抛物线
,-1,0、1、3的6张卡片,背面完全相同,洗匀后,从中任取两张,该卡片上的数分别作为点P 的横坐标和纵坐标,P落在抛物线 与对称轴右侧所围成的区域内(不含边界)的概率是 。
与对称轴右侧所围成的区域内(不含边界)的概率是 。查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
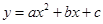 图象的一部分,图象过
图象的一部分,图象过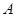 点(3,0),二次函数图象对称轴为
点(3,0),二次函数图象对称轴为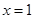 ,给出四个结论:①
,给出四个结论:①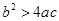 ;②
;②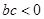 ;③
;③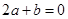 ;④
;④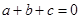 ,其中正确结论是( )
,其中正确结论是( )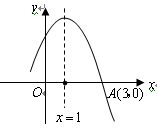
| A.②④ | B.①③ | C.②③ | D.①④ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
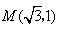 出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长
出发,沿射线OM方向以每秒1个单位长度的速度作匀速运动,在运动过程中,以OP为对角线的矩形OAPB的边长 ;过点O且垂直于射线OM的直线
;过点O且垂直于射线OM的直线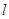 与点P同时出发,且与点P沿相同的方向、以相同的速度运动.
与点P同时出发,且与点P沿相同的方向、以相同的速度运动. 运动过程中,试判断AB与y轴的位置关系,并说明理由.
运动过程中,试判断AB与y轴的位置关系,并说明理由. 与直线L都运动了t秒,求此时的矩形OAPB与直线
与直线L都运动了t秒,求此时的矩形OAPB与直线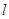 在运动过程中所扫过的区域的重叠部分的面积S(用含t的代数式表示).
在运动过程中所扫过的区域的重叠部分的面积S(用含t的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com