
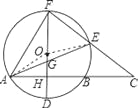
【题目】如图,⊙O的直径FD⊥弦AB于点H,E是![]() 上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.
上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.

(1)求⊙O的直径FD;
(2)在E点运动的过程中,EFCF的值是否为定值?若是,求出其定值;若不是,请说明理由;
(3)当E点运动到![]() 的中点时,连接AE交DF于点G,求△FEA的面积.
的中点时,连接AE交DF于点G,求△FEA的面积.
【答案】(1)DF=10;(2)是,EFCF=80;(3)S△FEA=30.
【解析】分析:(1)连接OA,由垂径定理得到AH=![]() AB=4,设OA=x,在Rt△OAH中,根据勾股定理列方程即可得到结论;(2)根据垂径定理得到
AB=4,设OA=x,在Rt△OAH中,根据勾股定理列方程即可得到结论;(2)根据垂径定理得到![]() ,根据圆周角定理得到∠BAF=∠AEF,推出△FAE∽△FCA,根据相似三角形的性质得到
,根据圆周角定理得到∠BAF=∠AEF,推出△FAE∽△FCA,根据相似三角形的性质得到![]() ,推出AF=EFCF,代入数据即可得到结论;(3)连接OE,由E点是
,推出AF=EFCF,代入数据即可得到结论;(3)连接OE,由E点是![]() 的中点,得到∠FAE=45°,∠EOF=90°,于是得到∠EOH=∠AHG,推出△OGE∽△HGA,根据相似三角形的性质得到
的中点,得到∠FAE=45°,∠EOF=90°,于是得到∠EOH=∠AHG,推出△OGE∽△HGA,根据相似三角形的性质得到![]() ,求得OG=
,求得OG=![]() ,得到FG=OF+OG=
,得到FG=OF+OG=![]() ,根据三角形的面积公式即可得到结论.
,根据三角形的面积公式即可得到结论.
本题解析:(1)连接OA,∵直径FD⊥弦AB于点H,∴AH=![]() AB=4,设OA=x,
AB=4,设OA=x,
在Rt△OAH中,AO2=AH2+![]() ,即x2=42+
,即x2=42+![]() ,∴x=5,
,∴x=5,
∴DF=2OA=10;
(2)是,
∵直径FD⊥弦AB于点H,∴![]() ,∴∠BAF=∠AEF,
,∴∠BAF=∠AEF,
∵∠AFE=∠CFA,∴△FAE∽△FCA,∴![]() ,∴AF2=EFCF,
,∴AF2=EFCF,
在Rt△AFH中,AF2=AH2+FH2=44+82=80,
∴EFCF=80;
(3)连接OE,∵E点是![]() 的中点,∴∠FAE=45°,∠EOF=90°,
的中点,∴∠FAE=45°,∠EOF=90°,
∴∠EOH=∠AHG,∵∠OGE=∠HGA,∴△OGE∽△HGA,
∴![]() ,即
,即![]()
![]() =
=![]() ,∴OG=
,∴OG=![]() ,∴FG=OF+OG=
,∴FG=OF+OG=![]() ,
,
∴S△FEA=S△EFG+S△AFG=![]() FGOE+
FGOE+![]() FGAH=
FGAH=![]() ×
×![]() ×(4+5)=30.
×(4+5)=30.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,M是线段AC的中点,N是线段BC的中点.
![]()
(1)如果AC=8cm,BC=6cm,求MN的长.
(2)如果AM=5cm,CN=2cm,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“4000辆自行车、187个服务网点”,台州市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地间的距离为448千米,一列慢车从A站出发,每小时行驶60千米,一列快车从B站出发,每小时行驶80千米.问:
(1)两车同时出发,相向而行,出发后多长时间相遇?
(2)两车相向而行,慢车先开28分钟,那么快车开出多长时间后两车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x+4分别交x轴,y轴于点A,C,点D(m,2)在直线AC上,点B在x轴正半轴上,且OB=3OC.点E是y轴上任意一点记点E为(0,n).
(1)求直线BC的关系式;
(2)连结DE,将线段DE绕点D按顺时针旋转90°得线段DG,作正方形DEFG,是否存在n的值,使正方形DEFG的顶点F落在△ABC的边上?若存在,求出所有的n值并直接写出此时正方形DEFG与△ABC重叠部分的面积;若不存在,请说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com