
分析 根据抛物线y=x2+bx+3与x轴的正半轴交于B、C两点,可设方程x2+bx+c=0的两个根为x1,x2,可求出b值,进而求出抛物线的顶点坐标.
解答 解:∵该抛物线与x轴的正半轴交于B、C两点,
∴设方程x2+bx+c=0的两个根为x1,x2,
∴x1+x2=-b,x1x2=3,
∵BC=4=|x1-x2|.
∴|x1-x2|=$\sqrt{({x}_{1}-{x}_{2})^{2}}$=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=4,
∴16=b2-12,
∵x1+x2=-b>0
∴b<0
∴b=-2$\sqrt{7}$,
∴y=x2-2$\sqrt{7}$x+3,
∴抛物线的顶点坐标为($\sqrt{7}$,-4).
点评 此题主要考查一元二次方程与函数的关系及三角形的面积公式,函数与x轴的交点的横坐标就是方程的根,两者互相转化,要充分运用这一点来解题.


科目:初中数学 来源: 题型:解答题
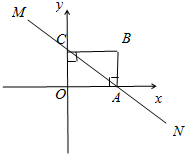 直线MN与x轴,y轴分别相交A、C两点,分别过A、C作x轴、y轴的垂线,二者相交于B点,且OA=8,OC=6.
直线MN与x轴,y轴分别相交A、C两点,分别过A、C作x轴、y轴的垂线,二者相交于B点,且OA=8,OC=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做损矩形的直径.
定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做损矩形的直径.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 35.9×105平方米 | B. | 3.60×105平方米 | C. | 3.59×105平方米 | D. | 35.9×104 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com