
【题目】如图,已知梯形ABCD中,AD∥BC,∠C=90°,以CD为直径的圆与AB相切,AB=6,求梯形ABCD的中位线长.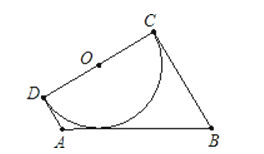
【答案】解:作OM⊥AB于M,连接OA、OB.
∵AD∥BC,∠C=90°,
∴∠D=180﹣∠C=90°,
∴以CD为直径的圆与AD、BC相切
∵以CD为直径的圆与AB相切,
∴AD=AM,BM=BC,
∴梯形ABCD的中位线长=![]() (AD+BC)=
(AD+BC)=![]() AB=3.
AB=3.
故梯形ABCD的中位线长为3.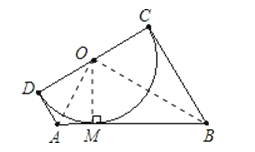
【解析】作OM⊥AB于M,连接OA、OB,证得AD=AM,BM=BC,用梯形的中位线定理求中位线长为3.
【考点精析】根据题目的已知条件,利用切线的性质定理的相关知识可以得到问题的答案,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】(1)如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB.
求证:CA+AD=BC.
小明为解决上面的问题作了如下思考:作△ADC关于直线CD的对称图形△A′DC,
∵CD平分∠ACB,∴A′点落在CB上,且CA′=CA,A′D=AD.因此,要证的问题转化为只要证A′D=A′B.请根据小明的思考写出该问题完整的证明过程.
(2)参照(1)中小明的思考方法,解答下列问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
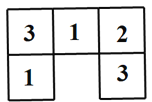
【题目】如图是一些棱长均为2cm的小立方块所搭几何体从上面看到的形状图,小正方形中的数字表示该位置的小立方块的个数.
(1)请画出从正面和左面看到的这个几何体形状图;
(2)这个几何体的体积是 cm3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积 S(单位:m2)与工作时间 t(单位:h)之间的函数关系 如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
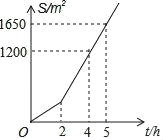
A. 150 m2 B. 300 m2 C. 330 m2 D. 450 m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3x2+3y2﹣5xy,B=2xy﹣3y2+4x2.
(1)化简:2B﹣A;
(2)已知﹣a|x﹣2|b2与![]() aby的同类项,求2B﹣A的值
aby的同类项,求2B﹣A的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=68°,则∠1+∠2=____°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB上 一点O,以O为端点画射线OC,作∠AOC的角平分线OD,作∠BOC的角平分线OE;

(1)按要求完成画图;
(2)通过观察、测量你发现∠DOE= °;
(3)补全以下证明过程:
证明:∵OD平分∠AOC(已知)
∴∠DOC= ∠AOC( )
∵OE平分∠BOC(已知)
∴∠EOC= ∠BOC( )
∵∠AOC+∠BOC= °
∴∠DOE=∠DOC+∠EOC= (∠AOC+∠BOC)= °.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com