
【题目】在△ABC中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD⊥MN于点D,BE⊥MN于点E。

(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你写出这个数量关系,并证明
【答案】(1)证明见详解;(2)证明见详解;(3)DE=BE-AD,理由见详解.
【解析】
(1)利用垂直的定义得∠ADC=∠CEB=90°,则根据互余得∠DAC+∠ACD=90°,再根据等角的余角相等得到∠DAC=∠BCE,然后根据“AAS”可判断△ADC≌△CEB,所以CD=BE,AD=CE,再利用等量代换得到DE=AD+BE;
(2)与(1)一样可证明△ADC≌△CEB,则CD=BE,AD=CE,于是有DE=CE-CD=AD-BE;
(3)与(1)一样可证明△ADC≌△CEB,则CD=BE,AD=CE,于是有DE=CD-CE=BE-AD.
(1)证明:∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠DAC+∠ACD=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB,
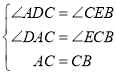 ,
,
∴△ADC≌△CEB(AAS),
∴CD=BE,AD=CE,
∴DE=CE+CD=AD+BE;
(2)证明:与(1)同理,可证明△ADC≌△CEB,
∴CD=BE,AD=CE,
∴DE=CE-CD=AD-BE;
(3)DE=BE-AD
证明:与(1)同理,可证明△ADC≌△CEB,
∴CD=BE,AD=CE,
∴DE=CD-CE=BE-AD.


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=45°,若BD=2,CD=3,AD⊥BC于D,将△ABD沿AB所在的直线折叠,使点D落在点E处;将△ACD沿AC所在的直线折叠,使点D落在点F处,分别延长EB、FC使其交于点M.
(1)判断四边形AEMF的形状,并给予证明.
(2)设AD=x,利用勾股定理,建立关于x的方程模型,求四边形AEMF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段![]() 和线段
和线段![]() .
.

(1)按要求作图(保留作围痕迹,不写作法);
延长线段![]() 至点
至点![]() ,使
,使![]() ,反向延长线段
,反向延长线段![]() 至点
至点![]() ,使
,使![]() ;
;
(2)如果![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,且
的中点,且![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间接到一批限期(可以提前)完成的零件加工任务.如果每天加工150个,则恰好按期完成;如果每天加工200个,则可比原计划提前5天完成.
(1)求这批零件的个数;
(2)车间按每天加工200个零件的速度加工了![]() 个零件后,提高了加工速度,每天加工250个零件,结果比原计划提前6天完成了生产任务,求
个零件后,提高了加工速度,每天加工250个零件,结果比原计划提前6天完成了生产任务,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”.为保护生态环境,A、B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:

(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元?
(2)在人均支出费用不变的情况下,为节约开支,两村准备协调40人共同清理养鱼网箱和捕鱼网箱.要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 经过
经过![]() 顶点
顶点![]() 的一条直线,
的一条直线,![]() .
.![]() 分别是直线
分别是直线![]() 上两点,且
上两点,且![]() .
.
(1)若直线![]() 经过
经过![]() 的内部,且
的内部,且![]() 在射线
在射线![]() 上,请解决下面两个问题:
上,请解决下面两个问题:
①如图1,若![]() ,
,![]() ,
,
则![]()
![]() ;
;![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”);
”);
②如图2,若![]() ,请添加一个关于
,请添加一个关于![]() 与
与![]() 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线![]() 经过
经过![]() 的外部,
的外部,![]() ,请提出
,请提出![]() 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
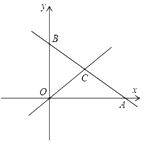
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() ,且点
,且点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
(1)点![]() 的坐标是________,点
的坐标是________,点![]() 的坐标是________;
的坐标是________;
(2)直线![]() 上有一点
上有一点![]() ,若
,若![]() ,试求出点
,试求出点![]() 的坐标;
的坐标;
(3)若点![]() 为直线
为直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 交于点
交于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() ,求
,求![]() 与
与![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com