
分析 分别利用负整数指数幂的性质以及结合有理数的乘方运算法则分别化简求出答案.
解答 解:-3-2=-$\frac{1}{9}$;
(-3)-2=$\frac{1}{9}$;
($\frac{1}{4}$)-2=$\frac{1}{(\frac{1}{4})^{2}}$=16;
(-$\frac{2}{3}$)2=$\frac{4}{9}$;
-$\frac{{2}^{2}}{3}$=-$\frac{4}{3}$;
-3-1=-$\frac{1}{3}$;
$\sqrt{9}$=3.
故答案为:-$\frac{1}{9}$,$\frac{1}{9}$,16,$\frac{4}{9}$,-$\frac{4}{3}$,-$\frac{1}{3}$,3.
点评 此题主要考查了负整数指数幂的性质以及有理数的乘方运算等知识,正确掌握运算法则是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,数轴上与1,$\sqrt{2}$对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是( )
如图,数轴上与1,$\sqrt{2}$对应的点分别为A,B,点B关于点A的对称点为C,设点C表示的数为x,则|x-$\sqrt{2}$|+$\frac{x}{\sqrt{2}}$的值是( )| A. | $\sqrt{2}-3$ | B. | 2$\sqrt{2}$-1 | C. | 3$\sqrt{2}$-3 | D. | 2-$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
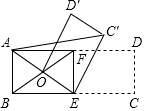 如图,已知点E、F是矩形ABCD的边BC、AD的中点,联结EF,将四边形ECDF绕点E逆时针旋转,点F正好与四边形ABEF对角线的交点O重合,得四边形OEC′D′,联结AC′,若AB=1,讨求线段AC′的长.
如图,已知点E、F是矩形ABCD的边BC、AD的中点,联结EF,将四边形ECDF绕点E逆时针旋转,点F正好与四边形ABEF对角线的交点O重合,得四边形OEC′D′,联结AC′,若AB=1,讨求线段AC′的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
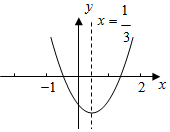 如图所示的二次函数 y=ax2+bx+c 的图象中,观察得出了下面五条信息:
如图所示的二次函数 y=ax2+bx+c 的图象中,观察得出了下面五条信息:| A. | ①②③ | B. | ①②④ | C. | ①②⑤ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com