
某楼盘一楼是车库(暂不出售),二楼至二十三楼均为商品房(对外销售),商品房售价方案如下:第八层售价为3 000元/米2,从第八层起每上升一层,每平方米的售价增加40元;反之,楼层每下降一层,每平方米的售价减少20元.已知商品房每套面积均为120平方米,开发商为购买者制定了两种购房方案:
方案一:购买者先交纳首付金额(商品房总价的30%),再办理分期付款(即贷款).
方案二:购买者若一次付清所有房款,则享受8%的优惠,并免收五年物业管理费(已知每月物业管理费为a元)
(1)请写出每平方米售价y(元/米2)与楼层x(2≤x≤23,x是正整数)之间的函数解析式.
(2)小张已筹到120 000元,若用方案一购房,他可以购买哪些楼层的商品房呢?
(3)有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算.你认为老王的说法一定正确吗?请用具体数据阐明你的看法.
(1)y=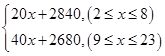 x为正整数
x为正整数
(2)小张用方案一可以购买二至十六层的任何一层
(3)见解析
解析解:(1)1°当2≤x≤8时,每平方米的售价应为:3 000-(8-x)×20=20x+2 840(元/平方米)
2°当9≤x≤23时,每平方米的售价应为:3 000+(x-8)·40=40x+2 680(元/平方米)
∴y=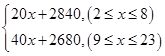 x为正整数.
x为正整数.
(2)由(1)知:
1°当2≤x≤8时,小张首付款为
(20x+2 840)·120·30%
=36(20x+2 840)≤36(20×8+2 840)=108 000元<12 0 000元
∴2~8层可任选.
2°当9≤x≤23时,小张首付款为(40x+2 680)×120×30%=36(40x+2 680)元
36(40x+2 680)≤120 000,解得x≤ =16
=16
∵x为正整数,∴9≤x≤16
综上得:小张用方案一可以购买二至十六层的任何一层.
(3)若按方案二购买第十六层,则老王要实交房款为:
y1=(40×16+2 680)×120×92%-60a(元)
若按老王的想法则要交房款为:
y2=(40×16+2 680)×120×91%(元)
∵y1-y2=3 984-60a
当y1>y2即y1-y2>0时,解得0<a<66.4,此时老王想法正确;
当y1≤y2即y1-y2≤0时,解得a≥66.4,此时老王想法不正确.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
如图,已知等腰△AOB放置在平面直角坐标系xOy中, OA=OB,点B的坐标为(3,4) .
(1)求直线AB的解析式;
(2)问将等腰△AOB沿x轴正方向平移多少个单位,能使点B落在反比例函数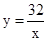 (x>0)的图象上.
(x>0)的图象上.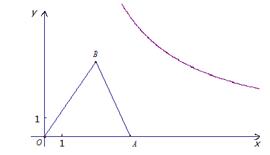
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
漳州三宝之一“水仙花”畅销全球,某花农要将规格相同的800件水仙花运往A,B,C三地销售,要求运往C地的件数是运往A地件数的3倍,各地的运费如下表所示:
| | A地 | B地 | C地 |
| 运费(元/件) | 20 | 10 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售, 售出土豆千克数与他手中持有的钱(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1) 农民自带的零钱是多少?
(2) 降价前他每千克土豆出售的价格是多少?
(3) 降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱) 是26元,问他一共带了多少千克土豆.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
“节能环保,低碳生活”是我们倡导的一种生活方式,某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台,三种家电的进价和售价如表所示:
| 价格种类 | 进价(元/台) | 售价(元/台) |
| 电视机 | 5000 | 5500 |
| 洗衣机 | 2000 | 2160 |
| 空调 | 2400 | 2700 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,梯形ABCD中,AB∥CD,AB=14,AD= 4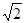 ,CD=7.直线l经过A,D两点,且sin∠DAB=
,CD=7.直线l经过A,D两点,且sin∠DAB=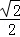 .动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.
.动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动,同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动,过点P作PM垂直于AB,与折线A→D→C相交于点M,当P,Q两点中有一点到达终点时,另一点也随之停止运动.设点P,Q运动的时间为t秒(t>0),△MPQ的面积为S.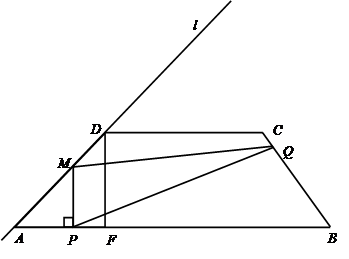
(1)求腰BC的长;
(2)当Q在BC上运动时,求S与t的函数关系式;
(3)在(2)的条件下,是否存在某一时刻t,使得△MPQ的面积S是梯形ABCD面积的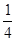 ?若存在,请求出t的值;若不存在,请说明理由;
?若存在,请求出t的值;若不存在,请说明理由;
(4)随着P,Q两点的运动,当点M在线段DC上运动时,设PM的延长线与直线l相交于点N,试探究:当t为何值时,△QMN为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y(件)与销售单价x(元)符合一次函数y=kx+b,且x=65时,y=55;x=75时,y=45.
(1)求一次函数y=kx+b的表达式;
(2)若该商场获得利润为W元,试写出利润W与销售单价x之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于500元,试确定销售单价x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
A、B两码头相距150千米,甲客船顺流由A航行到B,乙客船逆流由B到A,若甲、乙两客船在静水中的速度相同,同时出发,它们航行的路程y(千米)与航行时间x(时)的关系如图所示.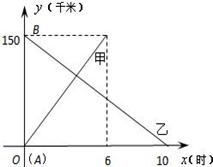
(1)求客船在静水中的速度及水流速度;
(2)一艘货轮由A码头顺流航行到B码头,货轮比客船早2小时出发,货轮在静水中的速度为10千米/时,在此坐标系中画出货轮航程y(千米)与时间x(时)的关系图象,并求货轮与客船乙相遇时距A码头的路程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com