
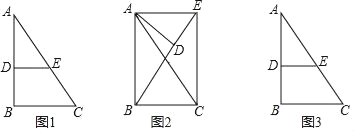
����Ŀ����1���۲췢�֣���ͼ1����Rt��ABC�У���B��90�㣬��D�ڱ�AB�ϣ���D��DE��BC��AC��E��AB��5��AD��3��AE��4����գ�
����ABC���ADE�Ƿ����ƣ���ֱ�ӻش��� ����
��AC���� ����DE���� ����
��2����չ̽��������ADE�ƶ���A��ת��ͼ2��ʾ��λ�ã������ADB���AEC�Ƿ����ƣ��������ƣ�˵�����ɣ������ƣ���֤����
��3��Ǩ��Ӧ�ã�����ADE�ƶ���A��ת����B��D��E��ͬһ��ֱ����ʱ��ֱ��д���߶�BE�ij���
���𰸡���1������������![]() ��
��![]() ����2����ADB�ס�AEC����3��4+
����2����ADB�ס�AEC����3��4+![]() ��4��
��4��![]() ��
��
��������
(1)�ٸ������������ε��ж��������
�ڸ��ݹ��ɶ������DE���������������ε������г�����ʽ�����AC��
(2)������ת�任�����ʵõ���BAD����CAE���������߶�Ӧ�ɱ������н���ȵ���������������֤����
(3)���ݹ��ɶ������BD��������������㼴�ɣ�
�⣺��1���١�DE��BC��
���ABC�ס�ADE��
�ʴ�Ϊ�����ƣ�
�ڡ�DE��BC��
���ADE����B��90�㣬
��DE��![]() ��
��![]() ��
��
�ߡ�ABC�ס�ADE��
��![]() ����
����![]() ��
��
��ã�AC��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��2����ADB�ס�AEC��
�������£�����ת�任�����ʿ�֪����BAD����CAE��
�ɣ�1���ã�![]() ���֡�BAD����CAE��
���֡�BAD����CAE��
���ADB�ס�AEC��
��3����ͼ2����Rt��ADB�У�BD��![]() ��4��
��4��
�ߵ�B��D��E��ͬһ��ֱ���ϣ�
��BE��BD+DE��4+![]() ��
��
��ͼ3��BE��BD��DE��4��![]() ��
��
��������������ADE�ƶ���A��ת����B��D��E��ͬһ��ֱ����ʱ���߶�BE�ij�Ϊ4+![]() ��4��
��4��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������M��y��ax2+bx+c��a��0������A����1��0�����Ҷ�������ΪB��0��1����
��1����������M�ĺ�������ʽ��
��2����F��t��0��Ϊx����������һ�㣬��������M�Ƶ�F��ת180��õ�������M1��
��������M1�Ķ���B1������Ϊ�� ����
����������M1���߶�AB�й�����ʱ����Ϻ�����ͼ����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b��ͼ����x�ύ�ڵ�A���뷴��������y=![]() ��x��0����ͼ���ڵ�B��2��n��������B��BC��x���ڵ�C����P��3n��4��1���Ǹ÷���������ͼ���ϵ�һ�㣬�ҡ�PBC=��ABC������������һ�κ����ı���ʽ��
��x��0����ͼ���ڵ�B��2��n��������B��BC��x���ڵ�C����P��3n��4��1���Ǹ÷���������ͼ���ϵ�һ�㣬�ҡ�PBC=��ABC������������һ�κ����ı���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+2x+m��2=0������ʵ������mΪ���������Ҹ÷��̵ĸ��������������������������������m�ĺ�Ϊ��������
A. 6 B. 5 C. 4 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y��kx+b��k��0���뷴��������y��![]() ��m��0����ͼ���ཻ��A��B���㣬����A��AD��x���ڵ�D��AO��5��OD��
��m��0����ͼ���ཻ��A��B���㣬����A��AD��x���ڵ�D��AO��5��OD��![]() AD��B�������Ϊ����6��n����
AD��B�����������6��n����
��1����һ�κ����ͷ����������ı���ʽ��
��2��P��y����һ�㣬�ҡ�AOP�ǵ��������Σ���ֱ��д�����з���������P�����꣮
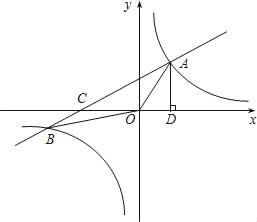
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��۵�����һ��AD,ʹ��D����BC�ߵĵ�F������֪�ۺ�AE=![]() ,��CE:CF=3:4,�����ABCD���ܳ�Ϊ����
,��CE:CF=3:4,�����ABCD���ܳ�Ϊ����
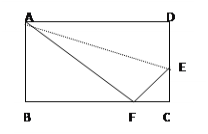
A. 36cm B. 3![]() C. 72cm D. 7
C. 72cm D. 7![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У���M������BC��һ�㣬��N��CD�ӳ�����һ�㣬��BM=DN��ֱ��BD��MN�ཻ��E��
��1����ͼ1������M��BC��ʱ����֤��BD��2DE=![]() BM��
BM��
��2����ͼ2������M��BC�ӳ�����ʱ��BD��DE��BM֮������Ĺ�ϵʽ��ʲô����
��3���ڣ�2���������£�����BN��AD�ڵ�F������MF��BD�ڵ�G����DE=![]() ����AF��FD=1��2ʱ�����߶�DG�ij���
����AF��FD=1��2ʱ�����߶�DG�ij���
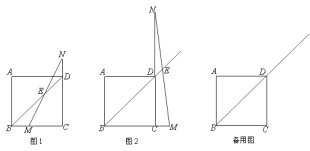
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ���װ��ֻ����ɫ��ͬ�ĺڡ���������ɫ����20ֻ��ijѧϰС��������ʵ�飬������Ⱥ�����������һ���������ɫ���ٰ����Żش��У������ظ����±�ʾ������е�һ��ͳ�����ݣ�
����Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1000 |
��������Ĵ���m | 58 | 96 | 116 | 295 | 484 | 601 |
���������Ƶ�� | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
�����ڴ��а���Լ��(���� )ֻ��
A. 8 B. 9 C. 12 D. 13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A������Ϊ��0��2������P��t��0����x���ϣ�B���߶�PA���е㣮���߶�PB���ŵ�P˳ʱ�뷽����ת90�㣬�õ��߶�PC������OB��BC��
��1���ж���PBC����״������Ҫ˵�����ɣ�
��2����t��0ʱ�����ʣ���P��O��B��CΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ������Ӧ��t��ֵ�������ܣ���˵�����ɣ�
��3����tΪ��ֵʱ����AOP����APC���ƣ�
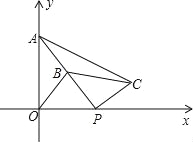
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com