
分析 设小红每消耗1千卡能量需要行走x步,则小明每消耗1千卡能量需要行走(x+2)步,根据数量关系消耗能量千卡数=行走步数÷每消耗1千卡能量需要行走步数结合小明步行12 000步与小红步行9 000步消耗的能量相同,即可得出关于x的分式方程,解之后经检验即可得出结论.
解答 解:设小红每消耗1千卡能量需要行走x步,则小明每消耗1千卡能量需要行走(x+2)步,
根据题意,得$\frac{12000}{x+2}$=$\frac{9000}{x}$,
解得x=6.
经检验:x=6是原方程的解.
答:小红每消耗1千卡能量需要行走6步.
点评 本题考查了分式方程的应用,根据数量关系消耗能量千卡数=行走步数÷每消耗1千卡能量需要行走步数列出关于x的分式方程是解题的关键.


 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源:2016-2017学年山东省文慧学校八年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列各式中,是一元一次不等式的是( )
A. 5+4>8 B. 2x-1=0 C. 2x≤5 D. 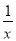 -3x≥0
-3x≥0
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
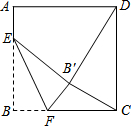 如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.
如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com