练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．如图，已知M是平行四边形ABCD中AB边的三等分点，BD与CM交于E，阴影部分面积为7，则平行四边形ABCD的面积为24．

    分析 由M是平行四边形ABCD中AB边的三等分点，易求得S△BEM：S△CDE=1：9，S△BEM：S△DEM=S△BEM：S△BCE=1：3，然后由阴影部分面积为7，求得各三角形的面积，继而求得答案．

    解答 解：∵四边形ABCD是平行四边形，
    ∴AB∥CD，AB=CD，
    ∴△BEM∽△DEC，
    ∵M是平行四边形ABCD中AB边的三等分点，
    ∴BM：CD=BE：DE=EM：CE，
    ∴S△BEM：S△CDE=1：9，S△BEM：S△DEM=S△BEM：S△BCE=1：3，
    ∵阴影部分面积为7，
    ∴S△BEM=1，
    ∴S△BCE=3，S△CDE=9，
    ∴S△BCD=S△BCE+S△CDE12，
    ∴S?ABCD=2S△BCD=24．
    故答案为：24．

    点评 此题考查了平行四边形的性质以及相似三角形的判定与性质．注意相似三角形的面积比等于相似比的平方，等高三角形的面积比等于对应底的比．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．解方程：
    （1）4x（x+3）+3（x+3）=0；         
    （2）x2+8x=9（用配方法）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知a、b、c是三角形的三边长，
    ①化简：|a-b-c|+|b-c-a|+|c-a-b|；
    ②若a+b=11，b+c=9，a+c=10，求这个三角形的各边．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，已知AD∥BE∥CF，它们依次交直线l1、l2于点A、B、C和点D、E、F．如果AB=6，BC=8，DF=21，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．用简便方法计算：
    （1）（$\frac{2}{3}$-$\frac{1}{4}$-$\frac{3}{8}$+$\frac{5}{24}$）×48
    （2）（-5）×3$\frac{1}{3}$+2×3$\frac{1}{3}$+（-6）×3$\frac{1}{3}$
    （3）-99$\frac{98}{99}$×9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

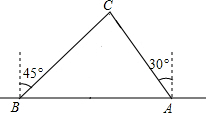    1．为了维护海洋权益，新组建的国家海洋局加大了在南海的巡逻力度，一天，我国两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻，同时发现一艘不明国籍的船只停在C处海域，如图，在B处测得C在东北方向上，在A处测得C在北偏西30°的方向上．
    （1）从A处看B、C两处的视角∠BAC=60度；
    （2）求从C处看A、B两处的视角∠ACB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

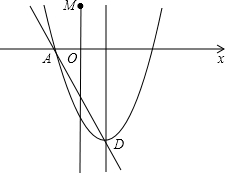    8．如图所示．抛物线y=x2+bx+c经过A（-1，0），B（4，5）两点．
    （1）求抛物线的解析式．
    （2）若抛物线的顶点为点D，对称轴所在的直线交x轴于点E，连接AD，点F为AD的中点．求出线段EF的长．
    （3）点M（0，2）在y轴上，点E在对称轴上，在直线AD上找一点F，使ME+EF最小，并求出点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知二次函数y=x2+bx+3的图象经过点（3，0）．
    （1）求b的值；
    （2）求出该二次函数顶点的坐标和对称轴；
    （3）在所给的坐标系中画出y=x2+bx+3的图象；
    （4）若抛物线y=x2+bx+3与坐标轴均有交点，请求出顺次连接抛物线顶点和抛物线与坐标轴交点构成的四边形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．计算：（+3）×（+4）=12，（+3）×（-4）=-12
    （-3）×（+4）=-12，（+3）×（-4）=-12．

    查看答案和解析>>

    同步练习册答案