
【题目】如图,直线AB与CD相交于点O,∠AOE=90°.
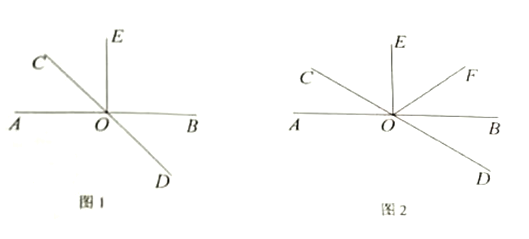
(1)如图1,若OC平分∠AOE,求∠AOD的度数;
(2)如图2,若∠BOC=4∠FOB,且OE平分∠FOC,求∠EOF的度数.
【答案】(1)135°;(2)54°
【解析】
(1)利用OC平分∠AOE,可得∠AOC=![]() ∠AOE=
∠AOE=![]() ×90°=45°,再利用∠AOC+∠AOD=180°,即可得出.
×90°=45°,再利用∠AOC+∠AOD=180°,即可得出.
(2)由∠BOC=4∠FOB,设∠FOB=x°,∠BOC=4x°,可得∠COF=∠COB-∠BOF=3x°,根据OE平分∠COF,可得∠COE=∠EOF=![]() ∠COF=
∠COF=![]() x°,即可得出.
x°,即可得出.
(1)∵∠AOE=90°,OC平分∠AOE,
∴∠AOC=![]() ∠AOE=
∠AOE=![]() ×90°=45°,
×90°=45°,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°-∠AOC=180°-45°=135°,
即∠AOD的度数为135°.
(2)∵∠BOC=4∠FOB,
∴设∠FOB=x°,∠BOC=4x°
∴∠COF=∠COB-∠BOF
=4x°-x°=3x°
∵OE平分∠COF
∴∠COE=∠EOF=![]() ∠COF=
∠COF=![]() x°
x°
∵![]() x+x=90°
x+x=90°
∴x=36,
∴∠EOF=![]() x°=
x°=![]() ×36°=54°
×36°=54°
即∠EOF的度数为54°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(1,0),点B(0, ![]() ),把△ABO绕点O顺时针旋转,得A′B′O,记旋转角为α.
),把△ABO绕点O顺时针旋转,得A′B′O,记旋转角为α.
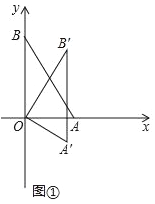
(Ⅰ)如图①,当α=30°时,求点B′的坐标;
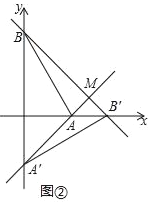
(Ⅱ)设直线AA′与直线BB′相交于点M.
如图②,当α=90°时,求点M的坐标;
②点C(﹣1,0),求线段CM长度的最小值.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项式乘方(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”.

根据“杨辉三角”请计算(a+b)64的展开式中第三项的系数为( )
A. 2016 B. 2017 C. 2018 D. 2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
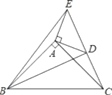
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
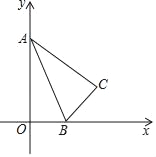
【题目】如图,Rt△ABC中,BC=4,AC=8,Rt△ABC的斜边在x轴的正半轴上,点A与原点重合,随着顶点A由O点出发沿y轴的正半轴方向滑动,点B也沿着x轴向点O滑动,直到与点O重合时运动结束.在这个运动过程中.
(1)AB中点P经过的路径长_____.
(2)点C运动的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠CAB=∠DBA,再添加一个条件,不一定能判定△ABC≌△BAD的是( )

A. AC=BDB. ∠1=∠2C. AD=BCD. ∠C=∠D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com