
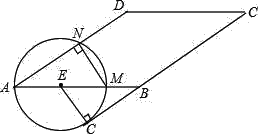
【题目】如图,在ABCD(AB>AD)中,点E在边AB上,以点E为圆心,AE长为半径的⊙E分别交AB、AD于点N、N,与BC所在的直线相切于点G
(1)求证:EG∥MN;
(2)若AB=10,AD与BC之间的距离为6,求⊙E的半径.
【答案】(1)见解析;(2)⊙E的半径为![]() .
.
【解析】
(1)根据平行四边形的性质可知∠1=∠2,根据直径所对的圆周角是直角可知∠ANM=90°,根据切线的性质可知∠BGE=90°,根据等角的余角相等可知∠3=∠4,即可证明EG∥MN;
(2)作AH⊥CG延长线于H,易证△BEG∽△BAH,根据对应边成比例得到BE与AE的数量关系,根据AE+EB=AB列方程求出AE即可.
如图所示,
∵四边形ABCD是平行四边形,
∴∠1=∠2,
∵AM是⊙E的直径,
∴∠ANM=90°,
∵BC所在的直线与⊙E相切于点G,
∴∠BGE=90°,
∴∠3=∠4,
∴EG∥MN;
(2)作AH⊥CG延长线于H,
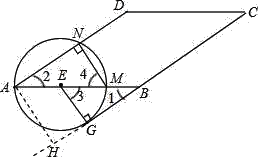
∵∠BGE=90°,
∴△BEG∽△BAH,
∴![]() ,
,
∵AE=GE,
∴![]() ,
,
∵AB=10,AH=6,
∴![]() ,
,
∴BE=![]() AE,
AE,
∵AE+EB=AB,
∴AE+![]() AE=10,
AE=10,
解得:AE=![]() ,
,
∴⊙E的半径为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,以点M(4,0)为圆心,MO为半径的半圆交x轴于点A,P为半圆上的一个动点,以点P为直角顶点在OP上方作Rt△OPB,且OP=2PB,OB交半圆于点Q.

(1)当P为半圆弧的中点时,求△OPB的面积.
(2)在运动过程中,求MB的最大值.
(3)在运动过程中,若点Q将线段OB分为1:2的两部分,求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏科版九年级下册数学课本65页有这样一道习题:
如图1,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.
(1)△ACD与△CBD相似吗?为什么?
(2)图中还有几对相似三角形?是哪几对?
复习时,小明提出了新的发现:“利用△ACD∽△CBD∽△ABC可以进一步证明:
①CD2=ADBD,②BC2=BDAB,③AC2=ADAB.”
(1)请你按照小明的思路,选择①、②、③中的一个进行证明;
(2)小亮研究“小明的发现”时,又惊喜地发现,利用“它”可以证明“勾股定理”,请你按照小亮思路完成这个证明;
(3)小丽也由小明发现的“CD2=ADBD”,进一步发现:“已知线段a、b,可以用尺规作图作出线段c,使c2=ab”,请你完成小丽的发现.(不要求写出作法,请保留作图痕迹)
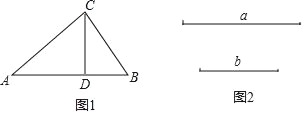
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长方体,它的长、宽、高分别为![]() 、
、![]() 、
、![]() .
.![]() 和
和![]() 是这个长方体上两个相对的顶点,点
是这个长方体上两个相对的顶点,点![]() 处有一只蚂蚁,想到点
处有一只蚂蚁,想到点![]() 处去吃可口的食物,则蚂蚁沿着长方体表面爬行到点
处去吃可口的食物,则蚂蚁沿着长方体表面爬行到点![]() 的最短路程为__________
的最短路程为__________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
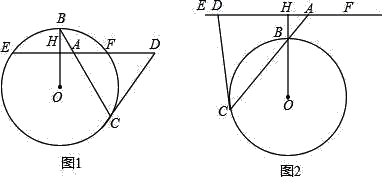
【题目】如图1,A为⊙O的弦EF上的一点,OB是和这条弦垂直的半径,垂足为H,BA的延长线交⊙O于点C,过点C作⊙O的切线与EF的延长线相交于点D.
(1)求证:DA=DC;
(2)当DF:EF=1:8,且DF=![]() 时,求ABAC的值;
时,求ABAC的值;
(3)将图1中的EF所在直线往上平行移动到⊙O外,如图2的位置,使EF与OB,延长线垂直,垂足为H,A为EF上异于H的一点,且AH小于⊙O的半径,AB的延长线交⊙O于C,过C作⊙O的切线交EF于D.试猜想DA=DC是否仍然成立?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE,PF分别交AB,AC于点E,F,给出下列四个结论:①△APE≌△CPF;②AE=CF;③△EAF是等腰直角三角形;④S△ABC=2S四边形AEPF,上述结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com