
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c②9a+3b+c>0:③b2<4ac④c=﹣3a⑤当y<0时,﹣1<x<3,其中正确的个数是_____(填序号).

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
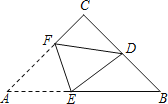
【题目】如图,在△ABC中,CA=CB,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么sin∠BED的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
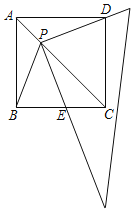
【题目】如图,一直角三角形的直角顶点P在边长为1的正方形ABCD对角线AC上运动(点P与A、C两点不重合)且它的一条直角边始终经过点D,另一直角边与射线BC交于点E.
(1)当点E在BC边上时,
①求证:△PBC≌△PDC;
②判断△PBE的形状,并说明理由;
(2)设AP=x,△PBE的面积为y.
①求出y关于x的函数关系式,并写出x的取值范围;
②当x取何值时,y取得最大值,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是ABCD的对角线,AB⊥BD,BD=8cm,AD=10cm,动点P从点D出发,以5cm/s的速度沿DA运动到终点A,同时动点Q从点B出发,沿折线BD-DC运动到终点C,在BD、DC上分别以8cm/s、6cm/s的速度运动.过点Q作QM⊥AB,交射线AB于点M,连接PQ,以PQ与QM为边作□PQMN.设点P的运动时间为t(s)(t>0),PQMN与ABCD重叠部分图形的面积为S(cm2).

(1)AP= cm(用含t的代数式表示).
(2)当点N落在边AB上时,求t的值.
(3)求S与t之间的函数关系式.
(4)连结NQ,当NQ与△ABD的一边平行时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
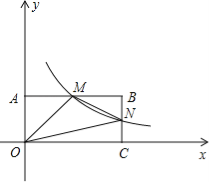
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
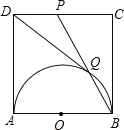
【题目】如图,AB是半圆O的直径,以AB为边在半圆同侧作正方形ABCD,点P是CD中点,BP与半圆交于点Q,连接DQ,设半圆的半径为a.
(1)判断直线DQ与半圆O的位置关系,并说明理由;
(2)求sin∠DQP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.

(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律,写出y1与t的函数关系式及自变量t的取值范围;
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2与时间t所符合的函数关系式,并写出相应自变量t的取值范围;
(3)设国内、外市场的日销售总量为y万件,写出y与时间t的函数关系式,并判断上市第几天国内、外市场的日销售总量y最大,并求出此时的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化校园,学校决定利用现有的2660盆甲种花卉和3000盆乙种花卉搭配A、B两种园艺造型共50个摆放在校园内,已知搭配一个A种造型需甲种花卉70盆,乙种花卉30盆,搭配一个B种造型需甲种花卉40盆,乙种花卉80盆.则符合要求的搭配方案有几种( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
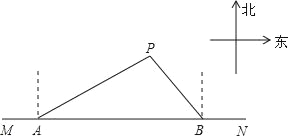
【题目】如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里(参考数据:sin32°≈0.53,sin55°≈0.82).
(1)求船P到海岸线MN的距离(精确到0.1海里);
(2)若船A、船B分别以20海里/小时、15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com