
分析 (1)把点的坐标代入解析式,求出a即可;
(2)根据二次函数的性质解答;
(3)把二次函数的顶点式化为一般式,根据y轴上点的坐标特征计算即可;
(4)根据二次函数的平移规律解答.
解答 解:(1)∵抛物线y=a(x+6)2经过点(1,-3),
∴-3=a(1+6)2,
解得,a=-$\frac{3}{49}$;
(2)抛物线开口向下,对称轴是x=-6,顶点坐标为(-6,0);
(3)∵y=-$\frac{3}{49}$(x+6)2=-$\frac{3}{49}$x2-$\frac{36}{49}$x-$\frac{108}{49}$,
∴抛物线与y轴的交点坐标为(0,-$\frac{108}{49}$);
(4)将此抛物线向右平移6个单位,再向上平移2个单位,平移后的抛物线的解析式为y=-$\frac{3}{49}$x2+2.
点评 本题考查的是二次函数的性质,二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上.
如图,把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图A(-4,0),C(0,3),将线段CA以点C为旋转中心旋转,所得的对应线段记为CA',当点A'落在y轴上时,写出A'的坐标,并求出以A'为顶点,经过A(-4,0)的抛物线的解析式.
如图A(-4,0),C(0,3),将线段CA以点C为旋转中心旋转,所得的对应线段记为CA',当点A'落在y轴上时,写出A'的坐标,并求出以A'为顶点,经过A(-4,0)的抛物线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x-1 | B. | y=-x+1 | C. | y=x+1 | D. | y=-x-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
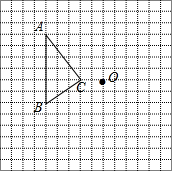 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).画出绕点O逆时针旋转 90° 后的△A′B′C′.
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).画出绕点O逆时针旋转 90° 后的△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 60° | B. | 120° | C. | 30° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的顶点C,D在反比例函数y=$\frac{8}{x}$(x>0)的图象上,顶点A,B分别在x轴和y轴的正半轴上,再在其右侧作正方形EFDG,顶点G在反比例函数y=$\frac{8}{x}$(x>0)的图象上,顶点E在x轴的正半轴上,则点G的坐标为(2$\sqrt{3}$+2,2$\sqrt{3}$-2).
如图,正方形ABCD的顶点C,D在反比例函数y=$\frac{8}{x}$(x>0)的图象上,顶点A,B分别在x轴和y轴的正半轴上,再在其右侧作正方形EFDG,顶点G在反比例函数y=$\frac{8}{x}$(x>0)的图象上,顶点E在x轴的正半轴上,则点G的坐标为(2$\sqrt{3}$+2,2$\sqrt{3}$-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 分数(分) | 人数(人) |
| 68 | 4 |
| 78 | 7 |
| 80 | 3 |
| 88 | 5 |
| 90 | 10 |
| 96 | 6 |
| 100 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图.线段AB的端点坐标分别为A(-6,0),B(0,2).点c从(0,4)出发以每秒2个单位的速度沿直线y=4向左平移,同时线段AB也沿x轴的正方向以每秒3个单位的速度平移.则经过$\frac{12}{5}$秒,△ABC的周长最小.
如图.线段AB的端点坐标分别为A(-6,0),B(0,2).点c从(0,4)出发以每秒2个单位的速度沿直线y=4向左平移,同时线段AB也沿x轴的正方向以每秒3个单位的速度平移.则经过$\frac{12}{5}$秒,△ABC的周长最小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com