
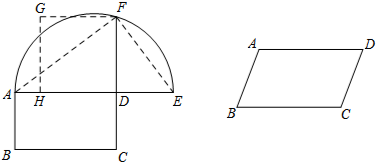
���� �ȸ���Բ�ܽǶ����õ���AFE=90�㣬��֤��Rt��AFD��Rt��FED�����������Ʊȿɵ�DF��DE=AD��DF��Ȼ����ݱ������ʵ�DF2=AD•CD��
������⣺����A��AM��BC�ڵ�M����ƽ���ı��ε����ΪAM��AD�ij˻���Ȼ�������Ŀ�ķ�����ͼ��
��� 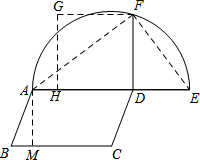 �⣺��AEΪֱ����
�⣺��AEΪֱ����
���AFE=90�㣬����AFD+��DFE=90�㣬
����DFE+��E=90�㣬
���E=��AFD��
��Rt��AFD��Rt��FED��
��DF��DE=AD��DF��
��DF2=AD•CD��
�ʴ�ΪDF2=AD•CD��
������⣺
����A��AM��BC�ڵ�M���ӳ�AD��E��ʹ��DE=AM����AEΪֱ������Բ������D��AE���ߣ�����Բ�ڵ�F����DFΪ����������DFGH��������DFGH��Ϊ������ͼ��
���� ���⿼��������-������ͼ��������ͼ�������ֻ�����ͼ�Ļ����Ͻ�����ͼ��һ���ǽ���˼���ͼ�ε����ʺͻ�����ͼ���������������Ŀ�Ĺؼ�����Ϥ��������ͼ�ε����ʣ���ϼ���ͼ�εĻ������ʰѸ�����ͼ���ɻ�����ͼ���������������Ĺؼ����������Ʊȵõ�DFΪAD��DE�ı������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 2 | C�� | $\sqrt{2}$ | D�� | 3$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
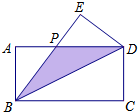 ��ͼ���ڳ�����ABCD�У��ѡ�BCD�ضԽ���BD�۵��õ���BED���߶�BE��AD�ཻ�ڵ�P����AB=2��BC=4��
��ͼ���ڳ�����ABCD�У��ѡ�BCD�ضԽ���BD�۵��õ���BED���߶�BE��AD�ཻ�ڵ�P����AB=2��BC=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
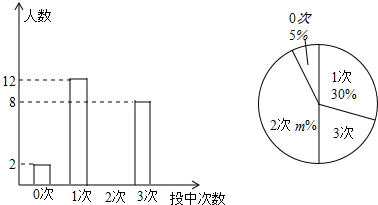
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6.5cm | B�� | 7cm | C�� | 7.5cm | D�� | 8cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12 | B�� | 3m+6 | C�� | -3m-12 | D�� | -3m+6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{{a}^{2}-2}$ | B�� | $\sqrt{{x}^{2}+2}$ | C�� | $\sqrt{3-��}$ | D�� | $\root{3}{a}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com