
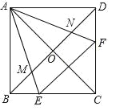
【题目】 如图,点E、F分别为正方形ABCD的边BC、CD上一点,AC、BD交于点O,且∠EAF=45°,AE,AF分别交对角线BD于点M,N,则有以下结论:①△AOM∽△ADF;②EF=BE+DF;③∠AEB=∠AEF=∠ANM;④S△AEF=2S△AMN,以上结论中,正确的个数有( )个.
A. 1B. 2C. 3D. 4
【答案】D
【解析】
如图,把△ADF绕点A顺时针旋转90°得到△ABH,由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF,由已知条件得到∠EAH=∠EAF=45°,根据全等三角形的性质得到EH=EF,所以∠ANM=∠AEB,则可求得②正确;
根据三角形的外角的性质得到①正确;
根据相似三角形的判定定理得到△OAM∽△DAF,故③正确;
根据相似三角形的性质得到∠AEN=∠ABD=45°,推出△AEN是等腰直角三角形,根据勾股定理得到AE=![]() AN,再根据相似三角形的性质得到EF=
AN,再根据相似三角形的性质得到EF=![]() MN,于是得到S△AEF=2S△AMN.故④正确.
MN,于是得到S△AEF=2S△AMN.故④正确.
如图,把△ADF绕点A顺时针旋转90°得到△ABH
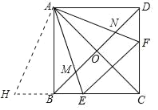
由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF
∵∠EAF=45°
∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=90°﹣∠EAF=45°
∴∠EAH=∠EAF=45°
在△AEF和△AEH中
∴△AEF≌△AEH(SAS)
∴EH=EF
∴∠AEB=∠AEF
∴BE+BH=BE+DF=EF,
故②正确
∵∠ANM=∠ADB+∠DAN=45°+∠DAN,
∠AEB=90°﹣∠BAE=90°﹣(∠HAE﹣∠BAH)=90°﹣(45°﹣∠BAH)=45°+∠BAH
∴∠ANM=∠AEB
∴∠ANM=∠AEB=∠ANM;
故③正确,
∵AC⊥BD
∴∠AOM=∠ADF=90°
∵∠MAO=45°﹣∠NAO,∠DAF=45°﹣∠NAO
∴△OAM∽△DAF
故①正确
连接NE,
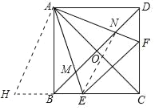
∵∠MAN=∠MBE=45°,∠AMN=∠BME
∴△AMN∽△BME
∴![]()
∴![]()
∵∠AMB=∠EMN
∴△AMB∽△NME
∴∠AEN=∠ABD=45°
∵∠EAN=45°
∴∠NAE=NEA=45°
∴△AEN是等腰直角三角形
∴AE=![]()
∵△AMN∽△BME,△AFE∽△BME
∴△AMN∽△AFE
∴![]()
∴![]()
∴![]()
∴S△AFE=2S△AMN
故④正确
故选D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
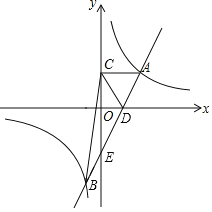
【题目】如图,直线y=ax﹣a与双曲线y=![]() (k>0)交于A、B两点,与x轴交于点D,与y轴交于点E,AC⊥y轴,垂足为点C.已知S△ACD=2,B(﹣1,m)
(k>0)交于A、B两点,与x轴交于点D,与y轴交于点E,AC⊥y轴,垂足为点C.已知S△ACD=2,B(﹣1,m)
(1)直接写出a与k的值.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线C1:y=ax2+bx﹣1经过点A(﹣2,1)和点B(﹣1,﹣1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M.
(1)求抛物线C1的表达式;
(2)直接用含t的代数式表达线段MN的长;
(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,防洪大堤的横断面是梯形,背水坡AB的坡比i=1:![]() ,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留三个有效数字,
,且AB=30m,李亮同学在大堤上A点处用高1.5m的测量仪测出高压电线杆CD顶端D的仰角为30°,己知地面BC宽30m,求高压电线杆CD的高度(结果保留三个有效数字,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
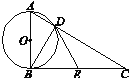
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC交于点D,E是BC的中点,连接BD,DE.
(1)若![]() ,求sinC;
,求sinC;
(2)求证:DE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用![]() 元购进某款智能清洁机器人进行销售,很快销售一空,商家又用
元购进某款智能清洁机器人进行销售,很快销售一空,商家又用![]() 元第二次购进同款智能清洁机器人,所购进数量是第一次的
元第二次购进同款智能清洁机器人,所购进数量是第一次的![]() 倍,但单价贵了
倍,但单价贵了![]() 元.
元.
(1)求该商家第一次购进智能清洁机器人多少台?
(2)若所有智能清洁机器人都按相同的标价销售,要求全部销售完毕的利润率不低于![]() (不考虑其它因素),那么每台智能清洁机器人的标价至少是多少元?
(不考虑其它因素),那么每台智能清洁机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,抛物线![]() 与x轴交于A,B两点,点P在该抛物线上(P点与A. B两点不重合),如果△ABP中PA与PB两条边的三边满足其中一边是另一边
与x轴交于A,B两点,点P在该抛物线上(P点与A. B两点不重合),如果△ABP中PA与PB两条边的三边满足其中一边是另一边![]() 倍,则称点P为抛物线
倍,则称点P为抛物线![]() 的“好”点.
的“好”点.
(1)命题:P(0,3)是抛物线![]() 的“好”点.该命题是_____( 真或假)命题.
的“好”点.该命题是_____( 真或假)命题.
(2)如图2,已知抛物线C:![]() 与
与![]() 轴交于A,B两点,点P(1,2)是抛物线C的“好”点,求抛物线C的函数表达式.
轴交于A,B两点,点P(1,2)是抛物线C的“好”点,求抛物线C的函数表达式.
(3)在(2)的条件下,点Q在抛物线C上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
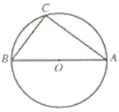
【题目】如图,⊙O的直径AB=10,弦AC=8,连接BC。
(1)尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法)
(2)在(1)所作的图中,求四边形ABCD的周长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com