
 如图,ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$.
如图,ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$.分析 (1)首先找出AC的中点O,然后以O为圆心,以AC长度的一半为半径,作出⊙O;然后标出⊙O与AB的交点D,与BC的交点E即可;
(2)如图2,连接OD,OE,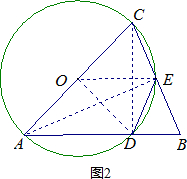 ,则OE∥AB,∠COE=∠BAC,∠DOE=∠ADO,判断出∠COE=∠DOE,然后根据圆心角定理,即可判断出$\overline{DE}=\overline{CE}$.
,则OE∥AB,∠COE=∠BAC,∠DOE=∠ADO,判断出∠COE=∠DOE,然后根据圆心角定理,即可判断出$\overline{DE}=\overline{CE}$.
(3)如图3,在Rt△ACE中,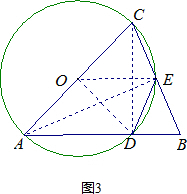 ,$cos∠ACB=\frac{CE}{AC}=\frac{\sqrt{5}}{5}$,AC=4$\sqrt{5}$,求出CE的长度是多少;然后求出DE=CE=4,在Rt△BCD中,求出BD的长度是多少,再用BC的长度加上BD的长度,求出△BDE的周长是多少即可.
,$cos∠ACB=\frac{CE}{AC}=\frac{\sqrt{5}}{5}$,AC=4$\sqrt{5}$,求出CE的长度是多少;然后求出DE=CE=4,在Rt△BCD中,求出BD的长度是多少,再用BC的长度加上BD的长度,求出△BDE的周长是多少即可.
解答 (1)解:如图1,⊙O为所求,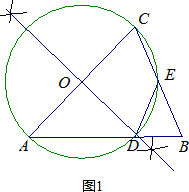 .
.
(2)证明:如图2,连接OD,OE, ,
,
则OE∥AB,∠COE=∠BAC,∠DOE=∠ADO,
又因为AO=DO,
所以∠BAC=∠ADO,
所以∠COE=∠DOE,
∴$\overline{DE}=\overline{CE}$.
(3)解:如图3,在Rt△ACE中, ,
,
$cos∠ACB=\frac{CE}{AC}=\frac{\sqrt{5}}{5}$,AC=4$\sqrt{5}$,
∴CE=AC•cos∠C=4$\sqrt{5}$×$\frac{\sqrt{5}}{5}$=4.
∵AB=AC,∠AEC=90°,
∴∠B=∠ACB,BE=CE=4.
又∵DE=CE,∴DE=CE=4.
在Rt△BCD中,$cos∠B=\frac{BD}{BC}$,
∵$cos∠B=cos∠ACB=\frac{\sqrt{5}}{5}$,BC=8,
∴BD=BC$•cos∠B=8×\frac{\sqrt{5}}{5}=\frac{8\sqrt{5}}{5}$,
∴△BDE的周长:l=BD+DE+BE=8+$\frac{8}{5}\sqrt{5}$.
点评 (1)此题主要考查了尺规作图的方法,解答此题的关键是熟悉基本几何图形的性质,结合几何图形的基本性质逐步操作.
(2)此题还考查了圆心角定理的应用,以及解直角三角形的方法的应用,要熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
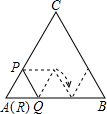 如图,正△ABC的边长为9cm,边长为3cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为6πcm.(结果保留π)
如图,正△ABC的边长为9cm,边长为3cm的正△RPQ的顶点R与点A重合,点P,Q分别在AC,AB上,将△RPQ沿着边AB,BC,CA连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动路径的长为6πcm.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
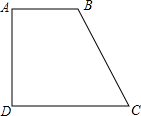 如图,在四边形ABCD中,AB∥CD,AB=12,BC=17,CD=20,AD=15.
如图,在四边形ABCD中,AB∥CD,AB=12,BC=17,CD=20,AD=15.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
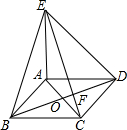 已知,已知?ABCD的对角线AC与BD相交于点O,△ABC和△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,连结BE,CE,且CE交BD于点F,现有四个结论:①BD=CE;②BD⊥CE;③∠ACE=∠ABE;④BF=EF,其中正确结论的个数为( )
已知,已知?ABCD的对角线AC与BD相交于点O,△ABC和△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,连结BE,CE,且CE交BD于点F,现有四个结论:①BD=CE;②BD⊥CE;③∠ACE=∠ABE;④BF=EF,其中正确结论的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 23×104 | B. | 2.3×104 | C. | 2.3×105 | D. | 2.3×10-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 利用某地七月份的日平均气温估计当地全年的日平均气温 | |
| B. | 为了解我国居民的年平均阅读时间,从大学生中随机抽取10万人进行抽查 | |
| C. | 调查某些七年级(1)班学生的身高;来估计该校全体学生的身高 | |
| D. | 为了了解一批洗衣粉的质量情况,从仓库中任意抽取100袋进行检验 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com