
如图,在⊿ ABC中,AE是中线,AD是角平分线,AF是高,∠ B=30°, ∠ C=80°, BE=2,AF=3,
填空:(1)AB= .(2)∠ BAD= (3)∠ DAF= (4)S⊿ AEC= .
 |
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
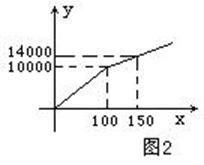
在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元)。现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购买门票的价格为每张60元;(总费用=广告赞助费+门票费)
方案二:购买方式如图2所示。
解答下列问题:
⑴分别求出方案一中y与x的函数关系式 和方案二中当x≥100时y与x的函数关系式.
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
下列各组图形中,是全等形的是( )
A.两个含60°角的直角三角形 B.腰对应相等的两个等腰直角三角形
C.边长为3和4的两个等腰三角形 D.一个钝角相等的两个等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
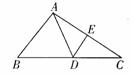
如图,DE是△ABC中边AC的垂直平分线,若BC=18 c m,AB=10 cm,则△ABD的周长为 ( )
m,AB=10 cm,则△ABD的周长为 ( )
A.16 cm B. 28 cm
28 cm
C.26 cm D.18 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
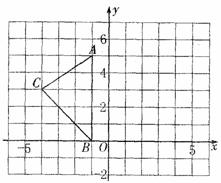
如图,在平面直角坐标系中,
A(-1,5),B(-1,0),C(-4,3).
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)写出点A1、B1、C1的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com