
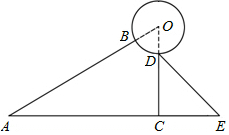
 如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=40$\sqrt{3}$厘米,∠CED=60°.
如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心O,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=40$\sqrt{3}$厘米,∠CED=60°.分析 (1)首先弄清题意,了解每条线段的长度与线段之间的关系,在△CDE中利用三角函数sin60°=$\frac{CD}{DE}$,求出CD的长.
(2)首先设出水箱半径OD的长度为x厘米,表示出CO,AO的长度,根据直角三角形的性质得到CO=$\frac{1}{2}$ AO,再代入数计算即可得到答案
解答 解:(1)∵DE=76厘米,∠CED=60°,
∴sin60°=$\frac{CD}{DE}$=$\frac{CD}{40\sqrt{3}}$,
∴CD=60cm.
(2)设水箱半径OD的长度为x厘米,则CO=(60+x)厘米,AO=(150+x)厘米,
∵∠BAC=30°,
∴CO=$\frac{1}{2}$AO,
60+x=$\frac{1}{2}$(150+x),
解得:x=30cm.
∴OD=30cm.
点评 本题考查勾股定理的应用、解直角三角形、锐角三角函数、直角三角形30度角性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x-y}{{{x^2}+{y^2}}}$ | B. | $\frac{xy-y}{3xy}$ | C. | $\frac{m-1}{1-m}$ | D. | $-\frac{61m}{32m}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
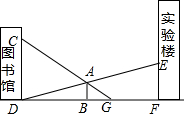 某中学的图书馆与实验楼中间有一地标牌AB,小鸣和小夕两位同学分别在图书馆和实验楼的C、E两点处观测地标牌的顶端A,他们的视线如图所示,小鸣从点C处可以看到地面上距离实验楼底部10米远的点G处,小夕从点E恰好可以看到图书馆的底部D处,已知图中的所有点均在同一平面内,CD⊥DF,AB⊥DF,EF⊥DF,CD=6米,EF=3米,DF=25米,请你根据以上数据,求该地标牌的高度AB及它与图书馆之间的距离BD(结果精确到0.1米).
某中学的图书馆与实验楼中间有一地标牌AB,小鸣和小夕两位同学分别在图书馆和实验楼的C、E两点处观测地标牌的顶端A,他们的视线如图所示,小鸣从点C处可以看到地面上距离实验楼底部10米远的点G处,小夕从点E恰好可以看到图书馆的底部D处,已知图中的所有点均在同一平面内,CD⊥DF,AB⊥DF,EF⊥DF,CD=6米,EF=3米,DF=25米,请你根据以上数据,求该地标牌的高度AB及它与图书馆之间的距离BD(结果精确到0.1米).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程x2+52=(x+1)2.
我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程x2+52=(x+1)2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
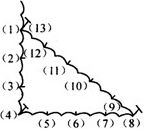 古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )| A. | 直角三角形两个锐角互补 | |
| B. | 三角形内角和等于180° | |
| C. | 如果三角形两条边长的平方和等于第三边长的平方 | |
| D. | 如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
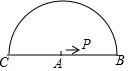 如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )
如图,半圆的直径CB=4,动点P从圆心A出发到B,再沿半圆周从B到C,然后从C回到A,按1单位/秒的速度运动.设运动时间为t(秒),PA的长为y(单位),y关于t的函数图象大致是( )| A. | 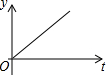 | B. | 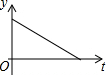 | C. | 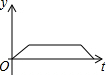 | D. | 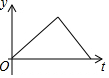 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com