
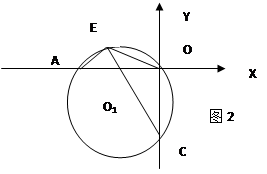
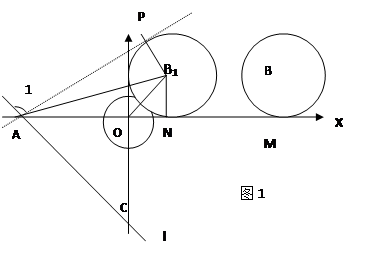
如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为![]() -1,直线l y=-X-
-1,直线l y=-X-![]() 与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.
与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.
(1) 求点A的坐标及∠CAO的度数;
(2) ⊙B以每秒1个单位长度的速度沿X轴负方向平移,同时,直线l绕点A顺时针匀速旋转.当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切.问:直线AC绕点A每秒旋转多少度?
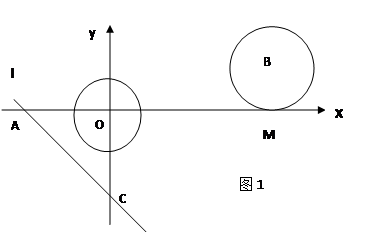
(3)如图2.过A,O,C三点作⊙O1,点E是劣弧![]() 上一点,连接EC,EA.EO,当点E在劣弧
上一点,连接EC,EA.EO,当点E在劣弧![]() 上运动时(不与A,O两点重合),
上运动时(不与A,O两点重合),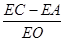 的值是否发生变化?如果不变,求其值,如果变化,说明理由.
的值是否发生变化?如果不变,求其值,如果变化,说明理由.
 .
.
【解析】(1)已知点A,C的坐标,故可推出OA=OC,最后可得∠CAO=45°.
(2)依题意,设⊙B平移t秒到⊙B1处与⊙O第一次相切,连接B1O,B1N,则MN=3.连接B1A,B1P可推出∠PAB1=∠NAB1.又因为OA=OB1=![]() ,故∠AB1O=∠NAB1,∠PAB1=∠AB1O继而推出PA∥B1O.然后在Rt△NOB1中∠B1ON=45°,∴∠PAN=45°得出∠1=90°.然后可得直线AC绕点A平均每秒30度.
,故∠AB1O=∠NAB1,∠PAB1=∠AB1O继而推出PA∥B1O.然后在Rt△NOB1中∠B1ON=45°,∴∠PAN=45°得出∠1=90°.然后可得直线AC绕点A平均每秒30度.
(3)在CE上截取CK=EA,连接OK,证明△OAE≌△OCK推出OE=OK,∠EOA=∠KOC,∠EOK=∠AOC=90°.最后可证明![]()
解:(1)、A(-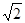 ,0)
,0)
∵C(0,-![]() ),∴OA=OC。
),∴OA=OC。
∵OA⊥OC ∴∠CAO=450----------------------------4分
(2)如图,设⊙B平移t秒到⊙B1处与⊙O第一次相切,此时,直线l旋转到l’恰好与⊙B1第一次相切于点P, ⊙B1与X轴相切于点N,
连接B1O,B1N,则MN=t, OB1= B1N⊥AN ∴MN=3 即t=3-------------2分
B1N⊥AN ∴MN=3 即t=3-------------2分
连接B1A, B1P 则B1P⊥AP B1P = B1N ∴∠PA B1=∠NAB1
∵OA= OB1=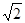 ∴∠A B1O=∠NAB1 ∴∠PA B1=∠A B1O ∴PA∥B1O
∴∠A B1O=∠NAB1 ∴∠PA B1=∠A B1O ∴PA∥B1O
在Rt⊿NOB1中,∠B1ON=450, ∴∠PAN=450, ∴∠1=900.
∴直线AC绕点A平均每秒300.------------------------------------4分
(3). ![]() 的值不变,等于
的值不变,等于![]() ,如图在CE上截取CK=EA,连接OK,
,如图在CE上截取CK=EA,连接OK,
∵∠OAE=∠OCK, OA=OC ∴⊿OAE≌⊿OCK,
∴OE=OK ∠EOA=∠KOC ∴∠EOK=∠AOC= 900.
∴EK=![]() EO ,
EO ,

|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 8 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
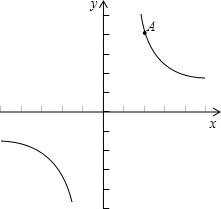
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y= (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=![]() .
.

1.求该反比例函数和一次函数的解析式
2.求△AOC的面积
查看答案和解析>>
科目:初中数学 来源:2010年北京市丰台区中考数学二模试卷(解析版) 题型:解答题
 的图象经过点A.正比例函数y=kx的图象绕原点顺时针旋转90°后,恰好经过点A,求k的值.
的图象经过点A.正比例函数y=kx的图象绕原点顺时针旋转90°后,恰好经过点A,求k的值.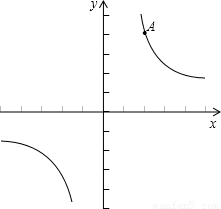
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(四川巴中卷)数学(解析版) 题型:解答题
如图,在平面直角坐标系中,一次函数 的图象与y轴交于点A,
的图象与y轴交于点A,
与x轴交于点B,与反比例函数 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
标为2,
(1)求一次函数和反比例函数的解析式;
(2)直接写出 时x的取值范围。
时x的取值范围。

查看答案和解析>>
科目:初中数学 来源:2013届湖南省八年级反比例函数测试数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=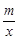 (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=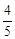 .
.
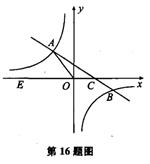
1.求该反比例函数和一次函数的解析式
2.求△AOC的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com