
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A(0,8),C(6,0).动点P从点B出发,以每秒1个单位长的速度沿射线BC方向匀速运动,设运动时间为t秒.
(1)当t= s时,以OB、OP为邻边的平行四边形是菱形;
(2)当点P在OB的垂直平分线上时,求t的值;
(3)将△OBP沿直线OP翻折,使点B的对应点D恰好落在x轴上,求t的值.

【答案】(1)16;(2)t=![]() ;(3)满足条件的t的值为5s或20s.
;(3)满足条件的t的值为5s或20s.
【解析】试题分析:(1)先有菱形的性质得出PC=BC=8,进而得出BP=16即可得出结论;
(2)由线段的垂直平分线的性质得出PO=PB=t,再利用勾股定理即可求出结论;
(3)分点P在x轴坐标轴和负半轴上,利用勾股定理即可建立方程求解.
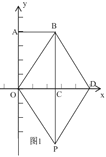
试题解析:(1)如图1,
∵A(0,8),∴OA=8,C(6,0),∴OC=6,
∵四边形OABC是矩形,∴BC=OA=8,
∵以OB、OP为邻边的平行四边形是菱形,∴CP=BC=OA=8,
∴BP=BC+CP=16,t=16÷1=16s,
故答案为16;
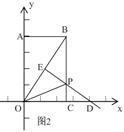
(2)如图2,∵点P是OB的垂直平分线上,∴PO=PB=t,∴PC=BC﹣PB=8﹣t,
在Rt△POC中,OC=6,根据勾股定理得,OC2+PC2=OP2,∴62+(8﹣t)2=t2,
∴t=![]() ;
;
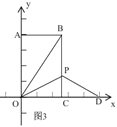
(3)当点P在x轴的坐标轴上时,如图3,
由折叠知,△OBP≌△ODP,∴PD=PB=t,OD=OB=![]() =10,∴CD=OD﹣OC=4,
=10,∴CD=OD﹣OC=4,
在Rt△PCD中,CD=4,PC=BC﹣PB=8﹣t,PD=t,
根据勾股定理得,PC2+CD2=PD2,∴42+(8﹣t)2=t2,∴t=5,
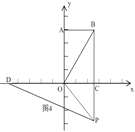
当点P在x轴负半轴上时,如图4,
由折叠知,PB=PD=t,OD=OB=10,∴CD=OD+OC=16,PC=t﹣8,
在Rt△PCD中,根据勾股定理得,PC2+CD2=PD2,∴(t﹣8)2+162=t2,∴t=20,
即:满足条件的t的值为5s或20s.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】两块大小一样斜边为4且含有30°角的三角板如图水平放置.将△CDE绕C点按逆时针方向旋转,当E点恰好落在AB上时,△CDE旋转了度,线段CE旋转过程中扫过的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了减少雾霾,美化环境,小王上班的交通方式由驾车改为骑自行车,小王家距单位的路程是15千米,在相同的路线上,小王驾车的速度是骑自行车速度的4倍,小王每天骑自行车上班比驾车上班要早出发45分钟,才能按原时间到达单位,求小王骑自行车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=30°,∠C=90°,E是斜边AB的中点,点P为AC边上一动点,若Rt△ABC的直角边AC=4,则PB+PE的最小值等于_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A(1,1),B(1,﹣1),C(﹣1,﹣1),D(﹣1,1),y轴上有一点P(0,2),作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称点P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此规律操作下去,则点P2017的坐标为( )

A. (2,0) B. (0,2) C. (0,﹣2) D. (﹣2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD﹣AB=2时,S2﹣S1的值为_______.(用a、b的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请仔细阅读下面材料,然后解决问题:
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”.例如: ![]() ,
, ![]() ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如: ![]() ,
, ![]() .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如: ![]() ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如: ![]() .
.
(1)将分式![]() 化为带分式;
化为带分式;
(2)当x取哪些整数值时,分式![]() 的值也是整数?
的值也是整数?
(3)当x的值变化时,分式![]() 的最大值为 .
的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=x+b,它的图象与两坐标轴所围成的图形的面积等于2.
(1)求b的值;
(2)若函数y=x+b的图象交y轴于正半轴,则当x取何值时,y的值是正数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com