
【题目】如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为 ![]() .其中,正确的结论是( )
.其中,正确的结论是( ) 
A.①②④
B.①③⑤
C.②③④
D.①④⑤
【答案】D
【解析】解:∵△ABC、△DCE都是等腰Rt△, ∴AB=AC= ![]() BC=
BC= ![]() ,CD=DE=
,CD=DE= ![]() CE;
CE;
∠B=∠ACB=∠DEC=∠DCE=45°;
①∵∠ACB=∠DCE=45°,
∴∠ACB﹣∠ACE=∠DCE﹣∠ACE;
即∠ECB=∠DCA;故①正确;
②当B、E重合时,A、D重合,此时DE⊥AC;
当B、E不重合时,A、D也不重合,由于∠BAC、∠EDC都是直角,则∠AFE、∠DFC必为锐角;
故②不完全正确;
④∵ ![]() ,∴
,∴ ![]() ;
;
由①知∠ECB=∠DCA,∴△BEC∽△ADC;
∴∠DAC=∠B=45°;
∴∠DAC=∠BCA=45°,即AD∥BC,故④正确;
③由④知:∠DAC=45°,则∠EAD=135°;
∠BEC=∠EAC+∠ECA=90°+∠ECA;
∵∠ECA<45°,∴∠BEC<135°,即∠BEC<∠EAD;
因此△EAD与△BEC不相似,故③错误;
⑤△ABC的面积为定值,若梯形ABCD的面积最大,则△ACD的面积最大;
△ACD中,AD边上的高为定值(即为1),若△ACD的面积最大,则AD的长最大;
由④的△BEC∽△ADC知:当AD最长时,BE也最长;
故梯形ABCD面积最大时,E、A重合,此时EC=AC= ![]() ,AD=1;
,AD=1;
故S梯形ABCD= ![]() (1+2)×1=
(1+2)×1= ![]() ,故⑤正确;
,故⑤正确;
因此本题正确的结论是①④⑤,故选D.
首先根据已知条件看能得到哪些等量条件,然后根据得出的条件来判断各结论是否正确.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为 . 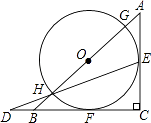
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图□ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=600,AB=![]() BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=
BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=![]() BC 成立的个数有( )
BC 成立的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,某校规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对该校七年级部分学生参加户外活动的时间进行调查,并将调查结果绘制成如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:

(1)填空:这次调查的学生共 人,表示户外活动时间为1小时的扇形圆心角度数是 度;
(2)求参加户外活动的时间为1.5小时的学生人数,并补全频数分布直方图;
(3)若该校七年级有学生600人,请估计该校七年级学生参加户外活动的时间不少于1小时的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )

A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从汽车灯的点O处发出的一束光线经灯的反光罩反射后沿CO方向平行射出,如入射光线OA的反射光线为AB,∠OAB=75°.在如图中所示的截面内,若入射光线OD经反光罩反射后沿DE射出,且∠ODE=22°.则∠AOD的度数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+b与双曲线y=![]() 相交于A(1,2)、B(m,-1)两点.
相交于A(1,2)、B(m,-1)两点.
(1)求直线和双曲线的解析式;
(2)若A1(x1,y1)、A2(x2,y2)、A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1、y2、y3的大小关系式;
(3)观察图象,请直接写出不等式k1x+b>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的例题:
解方程![]()
解:(1)当x≥0时,
原方程化为x2 – x –2=0,
解得:x1=2,x2= - 1(不合题意,舍去)
(2)当x<0时,
原方程化为x2 + x –2=0,
解得:x1=1,(不合题意,舍去)x2= -2
∴原方程的根是x1=2, x2= - 2
(3)请参照例题解方程![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com