
| A. | $\frac{{a}^{2}{+b}^{2}}{{a}^{2}{-b}^{2}}$ | B. | $\frac{{(a+b)}^{2}}{{a}^{2}{-b}^{2}}$ | C. | $\frac{{a}^{2}{-b}^{2}}{{a}^{2}{+b}^{2}}$ | D. | $\frac{{a}^{2}{+b}^{2}}{{(a-b)}^{2}}$ |
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
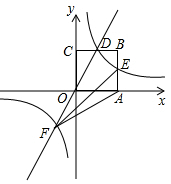 如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,点C分别在x轴,y轴的正半轴上,函数y=2x的图象与CB交于点D,函数y=$\frac{k}{x}$(k为常数,k≠0)的图象经过点D,与AB交于点E,与函数y=2x的图象在第三象限内交于点F,连接AF、EF.
如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,点C分别在x轴,y轴的正半轴上,函数y=2x的图象与CB交于点D,函数y=$\frac{k}{x}$(k为常数,k≠0)的图象经过点D,与AB交于点E,与函数y=2x的图象在第三象限内交于点F,连接AF、EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
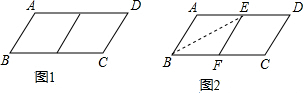 邻边不相等的平行四边形纸片,减去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,平行四边形ABCD中,若AB=1,BC=2,则平行四边形ABCD为1阶准菱形.
邻边不相等的平行四边形纸片,减去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,平行四边形ABCD中,若AB=1,BC=2,则平行四边形ABCD为1阶准菱形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
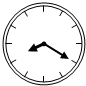 小明在他家里的时钟上安装了一个电脑软件,他设定当钟声在n点钟响起后,下一次则在(3n-1)小时后响起,例如钟声第一次在3点钟响起,那么第2次在(3×3-1=8)小时后,也就是11点响起,第3次在(3×11-1=32)小时后,即7点响起,以此类推…;现在第1次钟声响起时为2点钟,那么第3次响起时为3点,第2017次响起时为11点(如图钟表,时间为12小时制).
小明在他家里的时钟上安装了一个电脑软件,他设定当钟声在n点钟响起后,下一次则在(3n-1)小时后响起,例如钟声第一次在3点钟响起,那么第2次在(3×3-1=8)小时后,也就是11点响起,第3次在(3×11-1=32)小时后,即7点响起,以此类推…;现在第1次钟声响起时为2点钟,那么第3次响起时为3点,第2017次响起时为11点(如图钟表,时间为12小时制).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com