
分析 (1)利用二次根式的乘法法则运算;
(2)利用二次根式的乘法法则运算;
(3)利用完全平方公式计算;
(4)先把各二次根式化简为最简二次根式,然后合并即可;
(5)利用乘法公式展开,然后合并即可;
(6)利用零指数幂与负整数指数的意义计算.
解答 解:(1)$\sqrt{6}$×$\sqrt{\frac{2}{3}}$=$\sqrt{6×\frac{2}{3}}$=2;
(2)$\sqrt{27}$×$\sqrt{3}$-4=$\sqrt{27×3}$-4=9-4=5;
(3)($\sqrt{3}$-1)2=3-2$\sqrt{3}$+1=4-2$\sqrt{3}$;
(4)$\sqrt{27}$-$\frac{\sqrt{2}}{\sqrt{6}}$=3$\sqrt{3}$-$\frac{\sqrt{3}}{3}$=$\frac{8\sqrt{3}}{3}$;
(5)($\sqrt{3}$-$\sqrt{2}$)($\sqrt{2}$-$\sqrt{3}$)=$\sqrt{6}$-3-2+$\sqrt{6}$=2$\sqrt{6}$-5;
(6)(π-1)0+($\frac{\sqrt{3}}{2}$)-1+|5-$\sqrt{27}$|=1+$\frac{2\sqrt{3}}{3}$+3$\sqrt{3}$-5=$\frac{11\sqrt{3}}{3}$-4.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
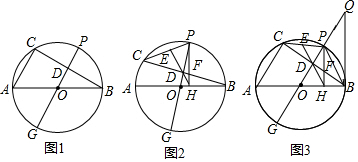
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
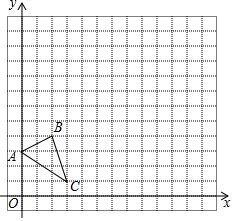 如图,
如图,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
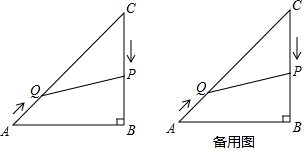
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
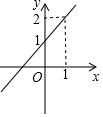 已知:一次函数的图象如图所示.
已知:一次函数的图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com