
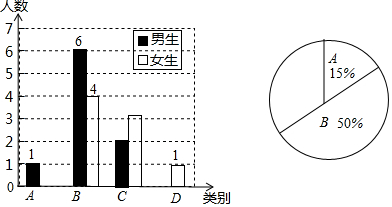
分析 (1)根据B类有6+4=10人,所占的比例是50%,据此即可求得总人数,再求得A类总人数可得A类女生人数,由各类别人数之和为总人数可得D类人数;
(2)利用(1)中求得的结果及对应人数除以总人数即为其百分比,补全图形即可得;
(3)利用列举法即可表示出各种情况,然后利用概率公式即可求解.
解答 解:(1)本次调查的学生数=(6+4)÷50%=20(名),
则A类女生有:20×15%-1=2(名),D类学生有20-(3+10+5)=2(名),
故答案为:20、2、2;
(2)C类百分比为$\frac{2+3}{20}$×100%=25%,D类别百分比为$\frac{2}{20}$×100%=10%,
补全图形如下: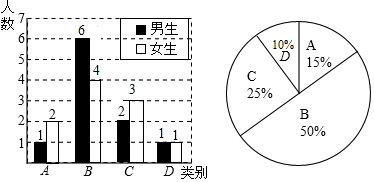
(3)由题意画树形图如下: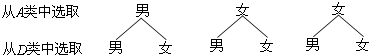
从树形图看出,所有可能出现的结果共有6种,且每种结果出现的可能性相等,所选一位女同学辅导一位男同学的结果共有2种.
所以P(一位女同学辅导一位男同学)=$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,点B在第一象限,直线y=x+1交y轴于点D,且点D为CO中点,将直线绕点D顺时针旋转15°经过点B,则点B的坐标为($\sqrt{3}$,2).
如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,点B在第一象限,直线y=x+1交y轴于点D,且点D为CO中点,将直线绕点D顺时针旋转15°经过点B,则点B的坐标为($\sqrt{3}$,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
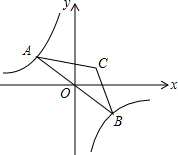 如图,已知反比例函数y=-$\frac{1}{x}$的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为y=$\frac{1}{3x}$.
如图,已知反比例函数y=-$\frac{1}{x}$的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为y=$\frac{1}{3x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
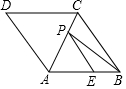 如图,菱形ABCD的边长为5,对角线AC=2$\sqrt{5}$,点E在边AB上,BE=2,点P是AC上的一个动点,则PB+PE的最小值为2$\sqrt{13}$.
如图,菱形ABCD的边长为5,对角线AC=2$\sqrt{5}$,点E在边AB上,BE=2,点P是AC上的一个动点,则PB+PE的最小值为2$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
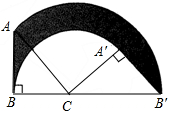 如图,等腰Rt△ABC中,∠B=90°,AB=1,将Rt△ABC绕点C按顺时针方向旋转,得到Rt△A′B′C,且B、C、B′三点共线,则边AB扫过的面积(图中阴影部分)是$\frac{3}{8}π$.
如图,等腰Rt△ABC中,∠B=90°,AB=1,将Rt△ABC绕点C按顺时针方向旋转,得到Rt△A′B′C,且B、C、B′三点共线,则边AB扫过的面积(图中阴影部分)是$\frac{3}{8}π$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com