
【题目】在△ABC中,AB=AC,∠BAC=α(0°<α<60°),分别以AB、BC为边作等边三角形ABE和等边三角形BCD,连结CE,如图1所示.
(1)直接写出∠ABD的大小(用含α的式子表示);
(2)判断DC与CE的位置关系,并加以证明;
(3)在(2)的条件下,连结DE,如图2,若∠DEC=45°,求α的值.
【答案】
(1)解:∵AB=AC,∠A=∠α,
∴∠ABC=∠ACB= ![]()
=90°﹣ ![]() ∠α
∠α
∴∠ABD=∠ABC﹣∠ABE
=90°﹣ ![]() ∠α﹣60°
∠α﹣60°
=30°﹣ ![]() ∠α
∠α
(2)解:DC与CE垂直;
连接AD;

∵∠ABE=∠DBC=60°,
∴∠ABE﹣∠DBE=∠DBC﹣∠DBE,
即∠ABD=∠EBC,
在△ABD和△EBC中,
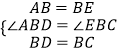 ,
,
∴△ABD≌△EBC,
∴∠ADB=∠ECB,
在△ABD和△ACD中,
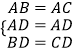 ,
,
∴△ABD≌△ACD,
∴∠BAD=∠CAD= ![]() ∠α,
∠α,
∴∠BDA=180°﹣∠ABD﹣∠BAD=180°﹣(30°﹣ ![]() ∠α )﹣
∠α )﹣ ![]() ∠α=150°,
∠α=150°,
∴∠BCE=150°,
∵∠BCD=60°,
∴∠DCE=90°,
即DC与CE垂直
(3)解:∵∠DCE=90°,
又∵∠DEC=45°,
∴△DEC为等腰三角形,
∴DC=DE=BC,
∵∠BCE=150°,
∴∠EBC=15°,
∵∠EBC=30°﹣ ![]() ∠α=15°,
∠α=15°,
∴∠α=30°
【解析】(1)用α的式子表示∠ABC,再利用∠ABD=∠ABC﹣60°;(2)连接AD,构造全等三角形,即△ABD≌△ACD,∠BDA=180°﹣∠ABD﹣∠BAD=180°﹣(30°﹣ ![]() ∠α )﹣
∠α )﹣ ![]() ∠α=150°,进而求出∠DCE=90°;(3)由已知可得△DEC为等腰三角形,DC=DE=BC,∠EBC=30°﹣
∠α=150°,进而求出∠DCE=90°;(3)由已知可得△DEC为等腰三角形,DC=DE=BC,∠EBC=30°﹣ ![]() ∠α=15°,进而∠α=30°
∠α=15°,进而∠α=30°


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
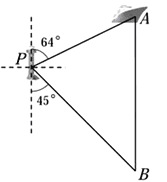
【题目】如图,一艘海轮位于灯塔![]() 的北偏东
的北偏东![]() 方向,距离灯塔120海里的
方向,距离灯塔120海里的![]() 处,它沿正南方向航行一段时间后,到达位于灯塔
处,它沿正南方向航行一段时间后,到达位于灯塔![]() 的南偏东
的南偏东![]() 方向上的
方向上的![]() 处,求
处,求![]() 和
和![]() 的长(结果取整数).
的长(结果取整数).
参考数据:![]() ,
,![]() 取
取![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现定义一种新运算“*”,规定a*b=ab+a﹣b,如1*3=1×3+1﹣3,则﹣2*5等于( )
A. 17B. 15C. ﹣17D. ﹣15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() .
.
(1)如图1,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,
上的点,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .若
.若![]() ,求证:
,求证:![]() ;
;
(2)如图2,![]() 是
是![]() 上的点,过点
上的点,过点![]() 作
作![]() ,交线段
,交线段![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .若
.若![]() ,
,
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 的长.
的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com