
【题目】如图,数轴上有三个点A、B、C,它们可以沿着数轴左右移动,请回答:
![]()
(1)将点B向右移动三个单位长度后到达点D,点D表示的数是 ;
(2)移动点A到达点E,使B、C、E三点的其中任意一点为连接另外两点之间线段的中点,请你直接写出所有点A移动的距离和方向;
(3)若A、B、C三个点移动后得到三个互不相等的有理数,它们既可以表示为1,![]() ,
,![]() 的形式,又可以表示为0,
的形式,又可以表示为0,![]() ,
,![]() 的形式,试求
的形式,试求![]() ,
,![]() 的值.
的值.
【答案】(1)1;(2)①向左移动3个单位长度;②向右移动4.5 单位长度;③向右移动12个单位长度;(3)![]() =-1,
=-1,![]() =1
=1
【解析】
试题(1)将点B向右移动三个单位长度后到达点D,则点D表示的数为-2+3=1;
(2)分类讨论:当点A向左移动时,则点B为线段AC的中点;当点A向右移动并且落在BC之间,则A点为BC的中点;当点A向右移动并且在线段BC的延长线上,则C点为BA的中点,然后根据中点的定义分别求出对应的A点表示的数,从而得到移动的距离;
(3)根据题意得到a≠0,a≠b,则有b=1,a+b=0,a=![]() ,即可求出a与b的值.
,即可求出a与b的值.
(1)由题意得点D表示的数是1;
(2)当点A向左移动时,则点B为线段AC的中点,
∵线段BC=3-(-2)=5,
∴点A距离点B有5个单位,
∴点A要向左移动3个单位长度;
当点A向右移动并且落在BC之间,则A点为BC的中点,
∴A点在B点右侧,距离B点2.5个单位,
∴点A要向右移动4.5 单位长度;
当点A向右移动并且在线段BC的延长线上,则C点为BA的中点,
∴点A要向右移动12个单位长度;
(3)依题意得:![]() ≠0,
≠0,![]() ≠
≠![]() ,显然有
,显然有![]() =1
=1
![]() +
+![]() =0,
=0,![]() =
=![]() ,
,
解得![]() =-1,
=-1,![]() =1的值.
=1的值.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从O出发,沿x轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t(秒),下列能反映S与t之间函数关系的图象是( )


A. A B. B C. C D. D
查看答案和解析>>
科目:初中数学 来源: 题型:
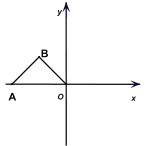
【题目】如图所示,在直角坐标系中,等腰直角![]() 的顶点
的顶点![]() 是坐标原点,点
是坐标原点,点![]() 的坐标是
的坐标是![]() ,直角顶点
,直角顶点![]() 在第二象限,把
在第二象限,把![]() 绕点
绕点![]() 旋转
旋转![]() 到
到![]() ,点
,点![]() 与
与![]() 对应,点
对应,点![]() 与
与![]() 对应,那么点
对应,那么点![]() 的坐标是_________.
的坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线![]() 经过点
经过点![]() 、
、![]() ,点
,点![]() 是第一象限的点且
是第一象限的点且![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() .
.

(1)求直线![]() 的解析式和点
的解析式和点![]() 的坐标;
的坐标;
(2)试说明:![]() ;
;
(3)若点![]() 是直线
是直线![]() 上的一个动点,在
上的一个动点,在![]() 轴上存在另一个点
轴上存在另一个点![]() ,且以
,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,请直接写出点
为顶点的四边形是平行四边形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在纸面上有一条数轴.
![]()
操作一:
(1)折叠纸面,使表示1的点与表示![]() 的点重合,则表示
的点重合,则表示![]() 的点与表示______的点重合.
的点与表示______的点重合.
操作二:
(2)折叠纸面,使表示![]() 的点与表示3的点重合,回答下列问题:
的点与表示3的点重合,回答下列问题:
①表示5的点与表示______的点重合;
②若数轴上A,B两点之间的距离为9(A在B的左侧),且折叠后A,B两点重合,求A,B两点表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几年前我国曾经流行有一种叫“二十四点”的数学趣味算题,方法是给出1~13之间的自然数,从中任取四个,将这四个数(四个数都只能用一次)进行“+”“-”“×”“÷”运算,可加括号使其结果等于24.
例如:对1,2,3,4可运算(1+2+3)×4=24,也可以写成4×(1+2+3)=24,但视作相同的方法.
现有郑、付两同学的手中分别握着四张扑克牌(见下图);若红桃、方块上的点数记为负数,黑桃、梅花上的点数记为正数.
请你对郑、付两同学的扑克牌的按要求进行记数,并按前面“二十四点”运算方式对郑、付两同学的记数分别进行列式计算,使其运算结果均为24.(分别尽可能提供多种算法)

依次记为:______ 、______ 、______ 、______

依次记为:______ 、______ 、______ 、______ .
(1)帮助郑同学列式计算:______
(2)帮助付同学列式计算:______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
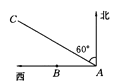
【题目】如图所示,某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时到达,到达后立即卸货,此时接到气象部门通知,一台风中心正以40海里/时的速度由A处向北偏西60°的AC方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响:
(1)B处是否会受到台风的影响?清说明理由;
(2)为避免卸货过程受到台风影响,船上人员应在多少小时内卸完货物?(精确到0.1小时, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com