
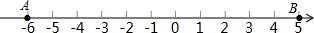 �Ķ����в��ϣ����ش����⣮
�Ķ����в��ϣ����ش����⣮���� ��1�����ݡ�|5-��-6��|�������������ϵ������DZ�ʾ5�ĵ����ʾ2�ĵ�֮��ľ�����лشɣ�
��2�����������ľ��뼴�ɽ��
��3��|x-2|�ļ����������������ϱ�ʾx�ĵ����ʾ2�ĵ�֮��ľ��룻
��4�����ݾ���ֵΪ�Ǹ�������3.4-|x-3|�����ֵ����|x-3|=0��
��� �⣺��1����|a-b|�ļ��������������ϱ�ʾa��b�����ľ��룬�ʴ�Ϊ�������ϱ�ʾa��b�����ľ��룻
��2������|a-b|�ļ���������֪|a-b|=|b-a|���ʴ�Ϊ��=��
��3��|x-2|�ļ����������������ϱ�ʾx�ĵ����ʾ2�ĵ�֮��ľ��룬
|x-2|=2��
x-2=2��x-2=-2��
��ã�x=4��0��
��4����3.4-|x-3|�����ֵ����|x-3|=0��
��ã�x=3��
���� ������Ҫ������Ǿ���ֵ�Ķ����Ӧ�ã����ⲢӦ�þ���ֵ�Ķ����ǽ���Ĺؼ���


 �������ϵ�д�
�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �� | B�� | �� | C�� | ƽ | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
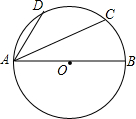 ��ͼ��A��B�ǡ�O��ֱ����C��D�ڡ�O�ϣ�$\widehat{AD}$=$\widehat{DC}$������DAB=58�㣬���CAB=��������
��ͼ��A��B�ǡ�O��ֱ����C��D�ڡ�O�ϣ�$\widehat{AD}$=$\widehat{DC}$������DAB=58�㣬���CAB=��������| A�� | 20�� | B�� | 22�� | C�� | 24�� | D�� | 26�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| $\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$ | ���ɣ� |
| $\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$ | |
| $\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$ | |
| �� | |
| $\sqrt{n+\frac{1}{n+2}}$=��n+1��$\sqrt{\frac{1}{n+2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
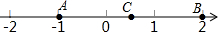 ��ͼ�������ϵĵ�A��B�ֱ��ʾ��-1��2����C���߶�AB���е㣬���C��ʾ������0.5��
��ͼ�������ϵĵ�A��B�ֱ��ʾ��-1��2����C���߶�AB���е㣬���C��ʾ������0.5���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com