
【题目】如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于点Q,PQ=3,PE=1.
(1)求证:∠ABE=∠CAD;
(2)求BP和AD的长.

【答案】(1)见解析;(2)7
【解析】
(1)根据SAS证明△ABE与△CAD全等即可得出结论;
(2)根据含30°的直角三角形的性质解答即可.
解:(1)证明:∵△ABC为等边三角形
∴AB=CA,∠BAE=∠C=60°
在△ABE和△CAD中
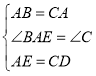
∴△ABE≌△CAD(SAS)
∴∠ABE=∠CAD
(2)在△ABP中,∠BPQ=∠ABP+∠BAP
∵∠ABP=∠CAD
∴∠BPQ=∠ABP+∠BAP=∠CAD+∠BAP=∠BAC=60°
∵BQ⊥AD,PQ=3,PE=1.
∴在Rt△BPQ中,∠BPQ=60°,则∠PBQ=30°.
∴BP=2PQ=6
∴BE=BP+PE=7.
由(1)△ABE≌△CAD,
∴AD=BE=7.


科目:初中数学 来源: 题型:
【题目】小明同学从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
①c<0;②abc>0;③2a﹣b=0;④a+b+c>0;⑤当﹣3<x<1时,y<0.
你认为其中正确信息的个数有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=18,BC=12,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则下列结论正确的个数是( )
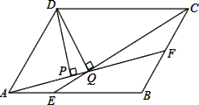
(1)CE平分∠BCD;(2)AF=CE;(3)连接DE、DF,则![]() ;(4)DP:DQ=
;(4)DP:DQ=![]()
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程组解应用题:用3辆![]() 型车和2辆
型车和2辆![]() 型车载满货物一次可运货17吨;用2辆
型车载满货物一次可运货17吨;用2辆![]() 型车和3辆
型车和3辆![]() 型车载满货物一次可运货18吨,某物流公司现有35吨货物,计划同时租用
型车载满货物一次可运货18吨,某物流公司现有35吨货物,计划同时租用![]() 型车
型车![]() 辆,
辆,![]() 型车
型车![]() 辆,一次运完,且恰好每辆车都载满货物.
辆,一次运完,且恰好每辆车都载满货物.
(1)1辆![]() 型车和1辆
型车和1辆![]() 型车都载满货物一次可分别运货多少吨?
型车都载满货物一次可分别运货多少吨?
(2)若![]() 型车每辆需租金200元/次,
型车每辆需租金200元/次,![]() 型车每辆需租金240元/次,请你帮该物流设计最省钱的租车方案,并求出最少租车费.
型车每辆需租金240元/次,请你帮该物流设计最省钱的租车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:把一张给定大小的矩形卡片ABCD放在宽度为10mm的横格纸中,恰好四个顶点都在横格线上,已知α=25°,求长方形卡片的周长。(精确到1mm,参考数据: sin25°≈0,cos25°≈0.9,tan25°≈0.5).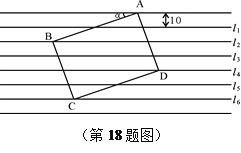
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小亮同学设计的一个轴对称图形的一部分.其中点![]() 都在直角坐标系网格的格点上,每个小正方形的边长都等于1.
都在直角坐标系网格的格点上,每个小正方形的边长都等于1.
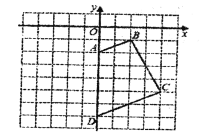
(1)请画出关于![]() 轴成轴对称图形的另一半,并写出
轴成轴对称图形的另一半,并写出![]() ,
,![]() 两点的对应点坐标.
两点的对应点坐标.
(2)记![]() ,
,![]() 两点的对应点分别为
两点的对应点分别为![]() ,
,![]() ,请直接写出封闭图形
,请直接写出封闭图形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则在下列各式子:①abc>0;②a+b+c>0;③a+c>b;④2a+b=0;⑤![]() =b2-4ac<0中,成立的式子有( )
=b2-4ac<0中,成立的式子有( )
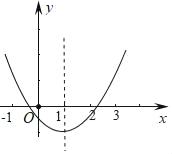
A. ②④⑤ B. ②③⑤
C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,BC=8 AB=6cm,动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
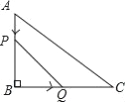
A. 18cm2 B. 12cm2 C. 9cm2 D. 3cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
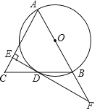
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,延长
的弦,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
![]() 求证:
求证:![]() 为
为![]() 的切线;
的切线;
![]() 猜想线段
猜想线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明你的猜想;
之间的数量关系,并证明你的猜想;
![]() 若
若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com