练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．下列图形，对称轴最多的是（　　）
    A．正方形B．等边三角形C．角D．线段

    分析 根据轴对称图形的对称轴的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线叫做轴对称图形的对称轴．

    解答 解：A、有4条对称轴，即两条对角线所在的直线和两组对边的垂直平分线；
    B、有3条对称轴，即各边的垂直平分线；
    C、有1条对称轴，即底边的垂直平分线；
    D、有2条对称轴．
    故选：A．

    点评 此题主要考查了轴对称图形的定义，轴对称图形的判断方法：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．这条直线是它的对称轴．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    10．如图，△ABC中，∠ACB=90°，AC=BC=2，现将一直角三角板的直角顶点放在AB的中点D处，两直角板所在的直线分别与直线AC、直线BC相交于点E、F．我们把DE⊥AC时的位置定为起始位置（如图①），将三角板绕点D顺时针方向旋转一个角度α（0°＜α＜90°）．若直线DE与直线BC交于点G，在旋转过程中，当△EFG为等腰三角形时，则FG=2或2$\sqrt{2}$．（注：若x2=a，且x＞0，则x=$\sqrt{a}$）

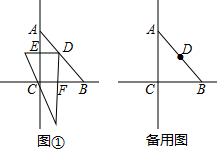
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

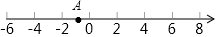    11．如图，已知点A在数轴上，从点A出发，沿数轴向右移动3个单位长度到达点C，点B所表示的有理数是5的相反数，按要求完成下列各小题．
    （1）请在数轴上标出点B和点C；
    （2）求点B所表示的有理数与点C所表示的有理数的乘积；
    （3）若将该数轴进行折叠，使得点A和点B重合，则点C和数-8所表示的点重合．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：
    （1）-8×2-（-10）
    （2）-9÷3-（$\frac{1}{2}$-$\frac{2}{3}$）×12-32．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如果2x2+ax-2y+7-（bx2-2x+9y-1）的值与x的取值无关，则-a-2b的值为（　　）
    A．3B．1C．2D．-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

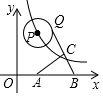    5．如图，动点P在函数y=$\frac{16}{x}$（x＞0）的图象上移动，⊙P半径为2，A（3，0），B（6，0），点Q是⊙P上的动点，点C是QB的中点，则AC的最小值是2$\sqrt{2}$-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

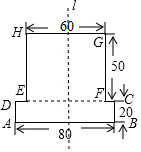    12．如图是由两个长方形组成的工件平面图（单位：mm），直线l是它的对称轴，若HG=60，AB=80，GF=50，CB=20，则能完全覆盖这个平面图形的圆面的最小半径是50mm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，在平面直角坐标系中，抛物线y=-$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x+3$\sqrt{3}$，分别交x轴于A、B两点，交y轴交于C点，顶点为D．
    （1）如图1，连接AD，R是抛物线对称轴上的一点，当AR⊥AD时，求点R的坐标；
    （2）在（1）的条件下．在直线AR上方，对称轴左侧的抛物线上找一点P，过P作PQ⊥x轴，交直线AR于点Q，点M是线段PQ的中点，过点M作MN∥AR交抛物线对称轴于点N，当平行四边形MNRQ周长最大时，在抛物线对称轴上找一点E，y轴上找一点F，使得PE+EF+FA最小，并求此时点E、F的坐标．
    （3）如图2，过抛物线顶点D作DH⊥AB于点H，将△DBH绕着H点顺时针旋转得到△D′B′H′且B′落在线段BD上，将线段AC直沿直线AC平移后，点A、C对应的点分别为A′、C′，连接D′C′，D′A′，△D′C′A′能否为等腰三角形？若能，请求出所有符合条件的点A′的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．（1）计算：|-2|-2sin30°+（-$\sqrt{3}$）2+（tan45°）-1
    （2）解方程：2x2-5x-3=0．

    查看答案和解析>>

    同步练习册答案